PRACTICE QUESTIONS ON COMBINATIONS

Question 1 :

If ⁽ⁿ⁺¹⁾C₈ : ⁽ⁿ⁻³⁾ P₄ = 57 : 16, find the value of n. 

Solution :

⁽ⁿ⁺¹⁾C₈  =  (n + 1)!/(n + 1 - 8)! 8! ==>  (n + 1)!/(n - 7)! 8!  --(1)

⁽ⁿ⁻³⁾ P₄ =  (n - 3)!/(n - 3 - 4)!  ==>  (n - 3)!/(n - 7)! --(2)

(1) : (2)

[(n + 1)!/(n - 7)! 8!] : [(n - 3)!/(n - 7)! ]  =  57 : 16

(n + 1)n(n - 1)(n - 2)/(8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2)  =  57 / 16

(n + 1) n (n - 1)(n - 2)  =  (57/16) ⋅ (8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2)

(n + 1) n (n - 1)(n - 2)  =  (57 ⋅  7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3) 

(n + 1) n (n - 1)(n - 2)  =  (3 ⋅ 19 ⋅  7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3) 

(n + 1) n (n - 1)(n - 2)  =  21 ⋅ 20 ⋅  19 ⋅ 18

n  =  20

Hence the value of n is 20.

Question 2 :

Prove that ²ⁿC_n = [2ⁿ × 1 × 3 × ·· · (2n − 1)] / n!.  

Solution :

L.H.S

  =  ²ⁿC_n  =  2n!/(2n-n)! n!  =  2n!/n! n!

  =  [2n (2n - 1)(2n - 2) .............  ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1] / n! n!

  =  [ 1 ⋅ 3 ⋅ 5 ⋅.............(2n - 1) ] [2 ⋅ 4 ⋅ 6 ⋅.......2n] / n! n!

  =  [ 1 ⋅ 3 ⋅ 5 ⋅.............(2n - 1) ] 2ⁿ [1 ⋅ 2 ⋅ 3 ⋅.......n] / n! n!

  =  [ 1 ⋅ 3 ⋅ 5 ⋅.............(2n - 1) ] 2ⁿ n! / n! n!

  =   2ⁿ [ 1 ⋅ 3 ⋅ 5 ⋅.............(2n - 1)] / n! ---> R.H.S

Hence it is proved.

Question 3 :

Prove that if 1 ≤ r ≤ n then n × ⁽ⁿ⁻¹⁾ C_r−1 = (n − r + 1) ⁿC_r−1.

Solution :

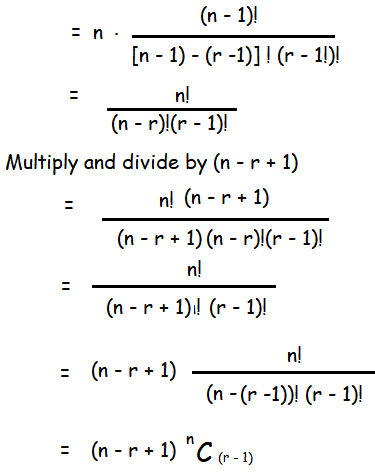
Question 4 :

Kabaddi coach has 14 players ready to play. How many different teams of 7 players could the coach put on the court?

Solution :

Number of ways of selecting 7 players out of 14 players 

=  ¹⁴C₇ 

=  14! / (14 - 7)! 7! 

=  14! / 7! 7!

=  (14 ⋅ 13 ⋅ 12 ⋅ 11 ⋅ 10 ⋅ 9 ⋅ 8 ⋅ 7!)/7! 7!

=  (14 ⋅ 13 ⋅ 12 ⋅ 11 ⋅ 10 ⋅ 9 ⋅ 8) / 7!

=  (14 ⋅ 13 ⋅ 12 ⋅ 11 ⋅ 10 ⋅ 9 ⋅ 8) / (7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2)

=  3432

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.