PRACTICE PROBLEMS USING HERONS FORMULA 

About "Practice Problems Using Herons Formula"

Practice Problems Using Herons Formula :

Here we are going to see some example problems to find the area triangle using herons formula.

Practice Problems Using Herons Formula - Practice questions

Question 1 :

The perimeter of a triangular plot is 600 m. If the sides are in the ratio 5 : 12 : 13, then find the area of the plot.

Solution :

The sides of triangle be 5x, 12x and 13x.

Perimeter of triangular plot  =  600

5x + 12x + 13x  =  600

30x  =  600

x  =  600/30  =  20

5x  =  5(20)  =  100

12x  =  12(20)  =  240

13x  =  13(20)  =  260

s  =  600/2  =  300

s - a  =  300 - 100  =  200

s - b  =  300 - 240  =  60

s - c  =  300 - 260  =  40

 √s(s − a)(s − b)(s − c)   =   √300(200)(60)(40) 

=   √(3 ⋅ 10 ⋅ 10 ⋅ 2 ⋅ 10 ⋅ 10 ⋅ 3 ⋅ 2 ⋅ 10 ⋅ 2 ⋅ 2 ⋅10)

   =  12000 m²

Question 2 :

Find the area of an equilateral triangle whose perimeter is 180 cm.

Solution :

Perimeter of equilateral triangle  =  180 cm

3a  =  180

a  =  180/3  =  60 cm

Area of equilateral triangle = (√3/4)a²

=  (√3/4)60²

=  900√3

=  900(1.732)

=  1558.8 cm²

Question 3 :

An advertisement board is in the form of an isosceles triangle with perimeter 36 m and each of the equal sides are 13 m. Find the cost of painting it at ₹ 17.50 per square metre.

Solution :

Let "x" be the unknown side of the triangle.

Then sides of triangle are x, 13 and 13.

perimeter   =  36 m

x + 13 + 13  =  36

x + 26  =  36

x  =  36 - 26  =  10 m

a = 10, b = 13 and c = 13

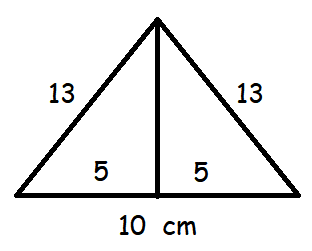
height  =  √13² - 5²

  =   √(169 - 25)

  =   √144

height   =  12 cm

Area of triangle  =  (1/2) x base x height

=  (1/2) x 10 x 12

  =  60 cm²

Cost of of painting it at ₹ 17.50 per square metre

 Required cost  =  60 (17.50)

  = ₹ 1050

After having gone through the stuff given above, we hope that the students would have understood, "Practice Problems Using Herons Formula"

Apart from the stuff given in this section,  if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.