PRACTICE PROBLEMS ON SPECIAL RIGHT TRIANGLES FOR SAT

Problem 1 :

In the figure given below, find the value of x.

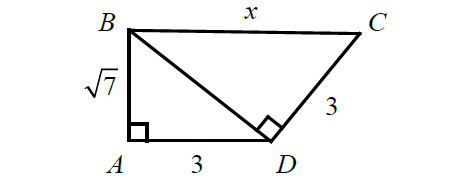
Solution :

In triangle ABD,

BD² = AB² + AD²

BD² = √7² + 3²

BD² = 7 + 9

BD² = 16

BD = 4

In triangle BDC,

BC² = BD² + DC²

x² = 4² + 3²

x² = 16 + 9

x² = 25

x = 5

Problem 2 :

In the figures below, find the values of x and y.

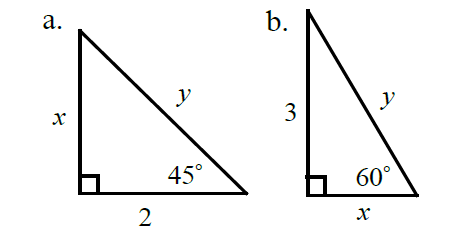
Solution :

(a) Since it is 45-45-90 triangle is an isosceles triangle, the value of x is 2.

In 45-45-90 right triangle, hypotenuse side = √2 ⋅ leg.

y = 2√2

(b) In a 30-60-90 right triangle,

longer leg = √3 ⋅ shorter leg

3 = √3 x

x = 3/√3

hypotenuse = 2⋅ shorter leg

y = 2x

y = 2(3/√3)

y = 2√3

Problem 3 :

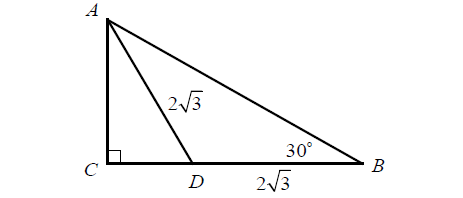
In the figure above, if AD = BD = 2√3, what is the length of AB?

Solution :

AD = BD = 2√3  (Given)

∠ADC = 30° + 30° (Using exterior angle theorem)

∠ADC = 60°

In triangle ADC,

∠CAD + ∠CDA + ∠ACD = 180°

∠CAD + 60° + 90° = 180°

∠CAD = 180°-150°

∠CAD = 30°

In triangle ACD, sine ∠CAD = 30°, its is a 30-60-90 triangle.

AD is hypotenuse and CD is the shorter leg.

hypotenuse (AD) = 2√3 (2 times the shorter leg)

CD = √3

The longer leg = (√3 times the shorter leg)

The longer leg(AC) = √3 √3

AC = 3

In triangle ABC,

BC = CD + BD

BC = √3 + 2√3 = 3√3

AB² = AC² + BC²

AB² = 3² + (3√3)²

AB² = 9 + 27

AB² = 36

AB = 6

So, length of AB is 6.

Problem 4 :

In the figure given above AB = 6, BC = 8 and CD = 5. What is the length of AD?

Solution :

In triangle ABC,

AC² = AB² + BC²

AC² = 6² + 8²

AC² = 36 + 64

AC = 10

In triangle ADC,

AC² = AD² + DC²

10² = AD² + 5²

AD² = 100 - 25

AD = √75

AD = 5√3

Problem 5 :

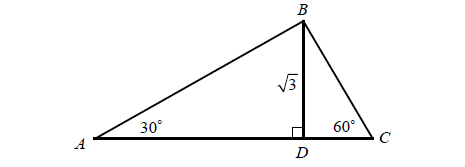
In the above triangle ABC, BD = √3. What is the perimeter of triangle ABC.

Solution :

In triangle BDC,

∠DBC  =  30

The side which is opposite to smaller angle is shorter, then, let DC = x.

BC = (2 times the shorter leg) = 2x

BC² = BD² + DC²

(2x)² = √3² + x²

3x² = 3

x² = 1

BC = 2(1)

= 2

DC = 1

In triangle ABD,

BD = √3 (Side which is opposite to smaller angle)

AB = 2√3 

AB² = AD² + BD²

(2√3)² =AD²+(√3)²

4(3) - 3 = AD²

12 - 3 = AD²

9 = AD²

3 = AD

CA = AD + DC

= 3 + 1

CA = 4

Perimeter of triangle ABC = AB + BC + CA

= 2√3 + 2 + 4

= 2√3 + 6

Problem 6 :

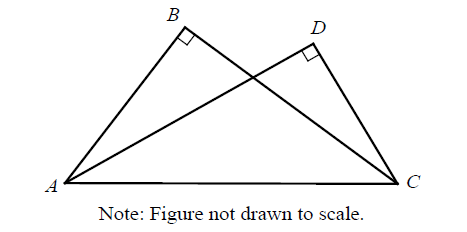
In the triangle above, ∠A ≅ ∠C and BD bisects AC. What is the perimeter of triangle ABC ?

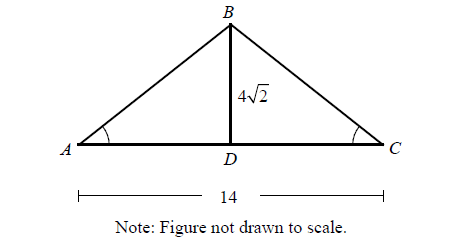
Solution :

Since BD is the bisector of AC,

AD = DC = 7

BD = 4√2

In triangle BDC,

BC² = BD² + DC²

BC² = (4√2)² + 7²

BC² = 16(2) + 49

BC² = 81

BC = 9

AB = 9

Perimeter of triangle ABC = AB + BC + CA

= 9 + 9 + 14

= 32

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.