PRACTICE PROBLEMS OF FINDING EQUATION OF THE LINE

Example 1 :

Find the equation of a straight line which has Slope -5/4 and passing through the point (–1, 2).

Solution :

Slope  =  -5/4

Equation of the line passing through the point (-1, 2)

y - y₁  =  m(x - x₁)

(y - 2)  =  (-5/4) (x - (-1))

4(y - 2)  =  - 5(x + 1)

4y - 2  =  -5x - 5

5x + 4y - 2 + 5  =  0

5x + 4y + 3  =  0

Example 2 :

You are downloading a song. The percent y (in decimal form) of mega bytes remaining to get downloaded in x seconds is given by y = −0.1x +1.

(i) graph the equation.

(ii) find the total MB of the song.

(iii) after how many seconds will 75% of the song gets downloaded?

(iv) after how many seconds the song will be downloaded completely?

Solution :

y = −0.1x +1

Points to be plotted :

(-10, 2) (0, 1) (10, 2)

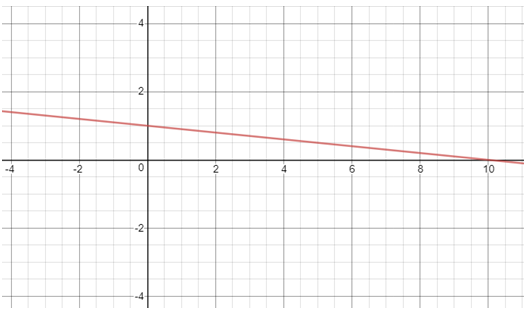
(ii) find the total MB of the song.

To find the total MB of the song, we have to assign the value of x as 0.(The initial point of downloading is at 0 seconds)

y = −0.1x +1

If x = 0

 y = -0.1(0) + 1

 y = 1

Hence the size of song to be downloaded is 1 MB.

(iii) after how many seconds will 75% of the song gets downloaded?

y = 75%  =  0.75

y = −0.1x +1

0.75  =  -0.1x + 1

0.75 - 1  =  -0.1x

-0.25  =  -0.1x

x  =  0.25/(0.1)

x  =  2.5 seconds 

Hence after 2.5 seconds 75% of the song gets downloaded.

(iv) after how many seconds the song will be downloaded completely?

Now, the size of MB is 0

0  =  -0.1 x + 1

0.1x  =  1

x  =  1/0.1  =  10

Hence it will take 10 seconds to download the song completely

Example 3 :

Find the equation of a line whose intercepts on the x and y axes are given below.

(i) 4, –6

Solution :

x intercept  =  a  =  4

y intercept  =  b  =  -6

(x/a) + (y/b)  =  1

(x/4) + (y/(-6))  =  1

(x/4) - (y/6)  =  1

(6x - 4y)/24  =  1

6x - 4y  =  24

3x - 2y  =  12

(ii)  -5, 3/4

x intercept  =  a  =  -5

y intercept  =  b  =  3/4

(x/a) + (y/b)  =  1

(x/(-5)) + (y/(3/4))  =  1

(-x/5) + (4y/3)  =  1

(-3x + 20y)/15  =  1

-3x + 20y  =  15

3x - 20y + 15  =  0

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.