PRACTICE PROBLEMS IN TRIGONOMETRY FOR GRADE 10

Problem 1 :

Determine whether the following is an identity or not.

cos²θ + sec²θ  =  2 + sinθ

Solution :

cos²θ + sec²θ :

=  1 - sin²θ + 1 + tan²θ

=  2 + tan²θ - sin²θ

≠  2 + sinθ

Because cos²θ + sec²θ  ≠  2 + sinθ, it's not an identity.

Problem 2 :

Determine whether the following is an identity or not.

cot²θ + cos θ  =  sin²θ

Solution :

cot²θ + cosθ :

=  cosec²θ - 1 + cosθ

≠  sin²θ

Because cot²θ + cos θ  ≠  sin²θ, it's not an identity.

Problem 3 :

Prove the following identity. 

sec²θ + cosec²θ  =  sec²θ ⋅ cosec²θ

Solution :

sec²θ + cosec²θ :

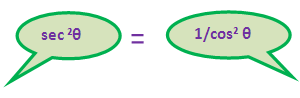
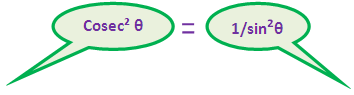
=  (1/cos²θ) + (1/sin²θ)

=  (sin²θ + cos²θ)/(cos²θ ⋅ sin²θ)

Value of sin²θ + cos²θ  =  1.

Then, 

=  1/(cos²θ sin²θ)

=  (1/cos²θ)(1/sin²θ)

=  sec²θ ⋅ cosec²θ

Problem 4 :

Prove the following identity. 

sin θ /(1 - cos θ)  =  cosec θ + cot θ

Solution :

sin θ /(1-cos θ) :

Multiply both numerator and denominator by the conjugate of the denominator. 

  =  [sin θ /(1-cos θ)] ⋅ [(1+cos θ)/(1+cos θ)]

Instead of (1 + cos θ)(1 + cos θ) we can write 1 - cos²θ by using the algebraic formula. 

=  [sin θ(1 + cosθ)]/(1-cos²θ)

=  [sin θ(1 + cosθ)]/sin²θ

=  (1 + cosθ)]/sinθ

=  (1/sinθ) + (cosθ/sinθ)

=  cosec θ + cot θ

Problem 5 :

Prove the following identity. 

√(1 - sin θ)/(1 + sin θ)  =  sec θ - tan θ

Solution :

√(1 - sin θ)/(1 + sin θ) :

=  √(1 - sin θ)/(1 + sin θ) ⋅ (1-sin θ)/(1-sin θ)

=  √(1 - sin θ)²/[(1 + sin θ) x (1 - sin θ)]

=  √(1 - sin θ)²/(1²- sin²θ)

=  √(1 - sin θ)²/(cos²θ)

=  √[(1 - sin θ)/(cosθ)]²

=  [(1 - sin θ)/(cosθ)]

=  [(1/cosθ) - (sin θ/cosθ)]

=  sec θ - tan θ

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.