PRACTICE PROBLEMS IN GEOMETRY FOR 9TH GRADE

Question 1 :

In the given, ∠A = 64° , ∠ABC = 58°. If BO and CO are the bisectors of ∠ABC and ∠ACB respectively of ΔABC, find x° and y°

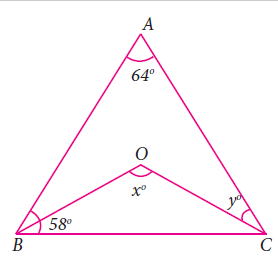
Solution :

Since BO and CO are bisectors of ABC and ACB.

<OBC  =  58/2  =  29

In triangle ABC,

<ABC + <BAC + <BCA  =  180

58 + 64 + <BCA  =  180

<BCA  =  180 - 122

<BCA  =  58

<y  =  58

In triangle OBC,

<OBC + <BOC + <BCO  =  180

29 + <BOC + 29  =  180

<BOC  =  180 - 58

x  =  <BOC  =  122

Question 2 :

In the given, if AB = 2, BC = 6, AE = 6, BF = 8, CE = 7, and CF = 7, compute the ratio of the area of quadrilateral ABDE to the area of ΔCDF.

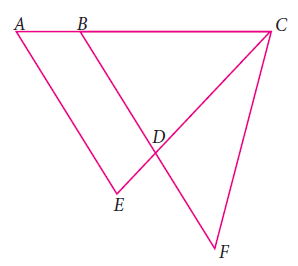
Solution :

Here we have three triangles, Δ AEC,  Δ BCF and Δ BDC.

Triangle BCD which is similar to ACE. 

In triangle AEC,

AC  =  AB + BC  =  2 + 6  =  8 cm

AE  =  6 cm and EC  =  7 cm

a  =  8, b = 6 and c = 7

Using a formula for area of scalene triangle

  =  √s(s - a) (s - b) (s - c)

  =  √10.5(2.5) (4.5) (3.5)

  =  √413.43

 =  20.33  ----(1)

In triangle BFC

BF  =  8 cm , BC  =   6 cm, and CF  =  7 cm

s  =  (8 + 6 + 7)/2  =  10.5

  =  √s(s - a) (s - b) (s - c)

  =  √10.5(2.5) (4.5) (3.5)

  =  √413.43

 =  20.33  ----(1)

Triangle BCD which is similar to ACE. 

And BCF  

To gets lengths BD and CD for triangle BCD we will use linear scale factor.  

We get lsf from lengths AC and BC as follows :

8/6 = 4/3

8(BF) /BD = 4/3

24 = 4BD

BD = 24/4 = 6 

CE/CD = 8/6

7/(CD) = 8/6

42 = 8CD

CD = 42/8

= 5.25

Area of BCD :

S  =  (6 + 6+, 5.25) /2  =  8.625

A  =  √8.625(8.625 - 6)(8.625 - 6)(8.625 - 5.25)

  = √200.58

  = 14.16

Area of CDF :

S = (5.25 + 7 + 2) / 2 = 7.125

A = √7.125(7.125 - 5.25) (7.125 - 7)(7.125 - 2)

  =  √8.558 = 2.925

   = 2.925

Area of ABDE. 

  =  20.33 - 14.16 = 6.17

The ratio of ABDE : CDF 

  =  6.17 : 2.925

Approximately : 6 : 3

  =  2 : 1

Question 3 :

In the figure, ABCD is a rectangle and EFGH is a parallelogram. Using the measurements given in the figure, what is the length d of the segment that is perpendicular to HE and FG?

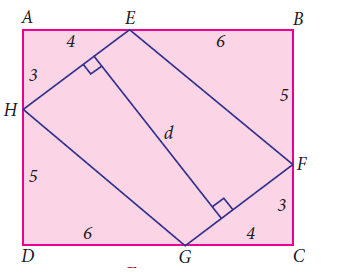
Question 4 :

In parallelogram ABCD of the accompanying diagram, line DP is drawn bisecting BC at N and meeting AB (extended) at P. From vertex C, line CQ is drawn bisecting side AD at M and meeting AB (extended) at Q. Lines DP and CQ meet at O. Show that the area of triangle QPO is 9/8  of the area of the parallelogram ABCD.

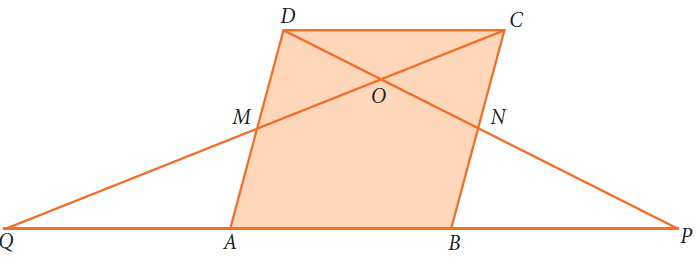
Solution :

[QPO]  =  [QAM] + [PBM] + [AMONB]  -----(1)

[QPO]  =  [AMONB] + [MDC] + [NCD]  -----(2)

From (2),

=  [AMONB] + [MDC] + [NOC] + [DOC]

= [ABCD] + [DOC]

Let  [ABCD] = K

= K + [DOC]

[DCNM ] is also a parallelogram.

So,

[DOC] = 1/4 [DCNM] , 2[ABCD] = [DCNM]

= 1/8 [ABCD] 

= k/8 

 [QPO] = K + K/8 

[ [QPO] = 9k/8 ]

Hence proved.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.