DIVISION ALGORITHM PROBLEMS

Problem 1 :

Prove that square of any integer leaves the remainder either 0 or 1 when divided by 4.

Solution :

Let n be the integer,  we wish to square.

Case 1 :

If n is even...

let n = 2m

n²  =  4m²

Hence n is divisible by 4 and leaves the remainder 0.

Case 2 :

If n is odd...

let n = 2m+1

n²  =  (2m + 1)²

n²  =  (2m)² + 2(2m) + 1²

n²  =  4m² + 4m + 1

n²  =  4(m² + m) + 1

Hence n is divisible by 4 and leaves the remainder 1.

Problem 2 :

Use Euclid’s Division Algorithm to find the Highest Common Factor (HCF) of

(i) 340 and 412

Solution :

a = 340 and b = 412

412 > 340

412  =  1 (340) + 72

340  =  4(72) + 52

72  =  1(52) + 20

52  =  2(20) + 12

20  =  1(12) + 8

12  =  1(8) + 4

8  =  2(4) + 0

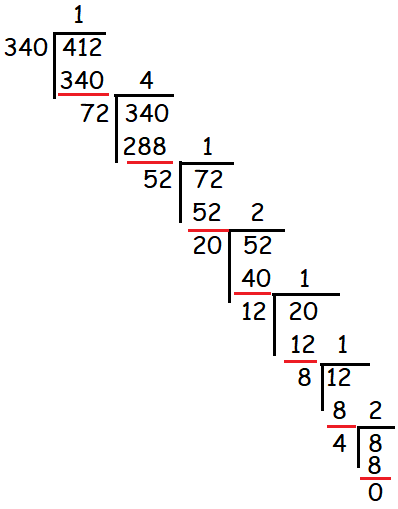
Hence the required H.C.F is 4.

(ii) 867 and 255

Solution :

a = 867 and b = 255

867 > 255

867  =  3(255) + 102

255  =  2(102) + 51

102  =  2(51) + 0

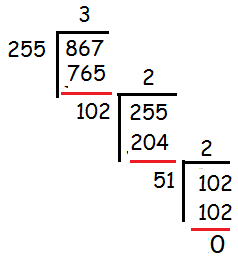
Hence the H.C.F is 51.

(iii)  10224 and 9648

Solution :

10224 > 9648

10224  =  1(9648) + 576

9648  =  16(576) + 432

576  =  1(432) + 144

432  =  3(144) + 0

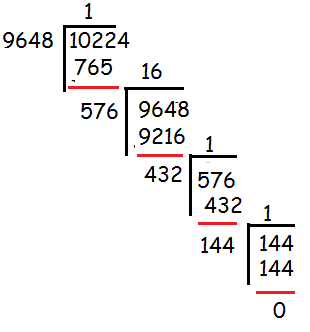
Hence the H.C.F is 144.

(iv) 84, 90 and 120

Solution :

90 > 84

90  =  1(84) + 6

84  =  6(14) + 0

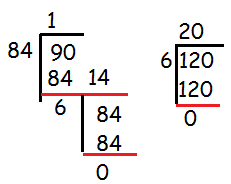
Hence the required H.C.F is 6.

Problem 3 :

Find the largest number which divides 1230 and 1926 leaving remainder 12 in each case.

Solution :

1230 - 12  =  1218

1926 - 12  =  1914

Now we have to find H.C.F of 1218 and 1914.

1914  =  1218(1) + 696

1218  =  696(1) + 522

696  =  522(1) + 174

522  =  174(3) + 0

Hence the largest number which divides 1230 and 1926 leaving remainder 12 is 174.

Problem 4 :

If d is the Highest Common Factor of 32 and 60, find x and y satisfying d = 32x + 60y .

Solution :

60 > 32

60  =  32(1) + 28 ----(1)

32  =  28(1) + 4 ----(2)

 28  =  4(7) + 0 ----(3)

Hence the H.C.F of 60 and 32 is 4.

d = 4

d = 32x + 60y 

4  =  32 x + 60 y

From (2), let us solve for 4

4  =  32 - 28(1) ---(4)

From (1), let us solve for 28

28  =  60 - 32(1)---(5)

By applying the value of 28 from (5) into (4), we get

4  =  32 - (60 - 32(1)) ⋅ 1

4  =  32 - 60 ⋅ 1 + 32 (1) ⋅ 1

4  =  32 + 32 (1) - 60 ⋅ 1 

4  =  32(1 + 1) - 60 ⋅ 1 

4  =  32(2) + 60 (-1) 

Instead of x, we have 2 and instead of y, we have -1.

Hence x = 2 and y = -1.

Problem 5 :

A positive integer when divided by 88 gives the remainder 61. What will be the remainder when the same number is divided by 11?

Solution :

Let "n" be that integer number.

We are given that (n-61) is divisible by 88.

Hence, (n-61) is divisible by 11.

It is the same as to say that ((n-55)-6) is divisible by 11. 

55 is divisible by 11

It means that the number n gives the remainder 6 when is divided by 11. 

Problem 6 :

Prove that two consecutive positive integers are always coprime.

Solution :

Let two consecutive numbers are x and x + 1

H.C.F of (x, x + 1) = n, because it cannot be equal to 1, n is natural and n > 1

n divides n both x and x + 1.

then n divides x + 1 - x

Hence n divides 1 or n = 1

But we have assumed n > 1

So by contradiction x & x + 1 are co-prime.

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.