PRACTICAL PROBLEMS USING SECTION FORMULA

Problem 1 :

Using the section formula, show that the points

A(1, 0),B (5, 3), C (2, 7) and D(-2, 4)

are vertices of a parallelogram taken in order.

Solution :

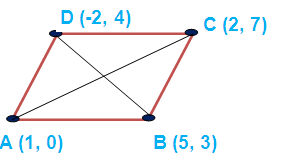
The midpoint of the diagonals AC and the diagonal BD coincide

Section formula internally

= (lx₂+mx₁)/(l+m), (ly₂+my₁)/(l+m)

l = 1 and m = 1

The midpoint of the diagonals AC. The midpoint of diagonal is in the ration 1:1

=  (1(2)+1(1))/(1+1) , ((1(7) + 1(0))/(1+1)

=  (2+1)/2 , (7+0)/2

=  (3/2, 7/2)   ------- (1)

The midpoint of the diagonals BD. The midpoint of diagonal is in the ration 1:1

=  ((1(-2)+1(5))/(1+1) , ((1(4) + 1(3))/(1+1)

=  (-2+5)/2 , (4+3)/2

=  (3/2, 7/2)    ------- (2)

Two diagonals are intersecting at the same point. So the given vertex forms a parallelogram.

Problem 2 :

The 4 vertices of a parallelogram are

A(-2, 3), B(3, -1), C(p, q) and D(-1, 9)

Find the value of  p and q.

Solution :

The midpoint of the diagonals AC and the diagonal BD coincide

Section formula internally

= (lx₂+mx₁)/(l+m), (ly₂+my₁)/(l+m)

l = 1 and m = 1

The midpoint of the diagonals AC. The midpoint of diagonal is in the ratio 1:1

=  (1(p)+1(-2))/(1+1) , ((1(q) + 1(3))/(1+1)

=  (p-2)/2 , (q+3)/2  ------- (1)

The midpoint of the diagonals BD. The midpoint of diagonal is in the ratio 1:1

=  ((1(-1)+1(3))/(1+1) , ((1(9) + 1(-1))/(1+1)

=  (-1+3)/2 , (9-1)/2

=  (1, 4)    ------- (2)

(1)  =  (2)

Equating x and y -coordinates, we get 

Problem 3 :

Find the coordinates of the point which divides the line segment joining

(3, 4) and (-6, 2)

in the ratio 3:2 externally.

Solution :

Section formula externally

=  (lx₂ - mx₁)/(l-m) , (ly₂-my₁)/(l-m)

A (3, 4) B (-6, 2)     3 : 2

l = 3 and m = 2    

=  (-18 - 6)/1 , (6 - 8)/1

=   (-24 , -2)

Problem 4 :

The coordinate of the midpoint of the line joining the point (2p, 4) and (-2, 2q) and (3, p). Find the value of q.

Solution :

The given problem can be done in two ways.

i) Using midpoint formula

ii) Using section formula

i) Finding the value of q, using midpoint formula :

(x₁ + x₂)/2, (y₁ + y₂)/2 = (3, p)

(2p + (-2))/2, (4 + 2q)/2 = (3, p)

(p - 1), (2 + q) = (3, p)

Equating the x and y-coordinates, we get

So, the value of q is 2.

ii) Finding the value of q using section formula  :

The point (3, p) is dividing the line segment in the ratio 1 : 1 internally.

= (lx₂ + mx₁) / (l + m), (my₂ + ny₁) / (m + n)

x₁ = 2p, y₁ = 4, x₂ = -2, y₂ = 2q

1(-2) + 1(2p) / (1 + 1), 1(2q) + 1(4) / (1 + 1) = (3, p)

(-2 + 2p) / 2, 2q + 4 / 2 = (3, p)

(-1 + p),  (q + 2) = (3, p)

Equating x and y-coordinates, we get

-1 + p = 3

p = 3 + 1 ==> 4

q + 2 = p

Applying the value of p, we get

q + 2 = 4

q = 4 - 2

q = 2

Problem 5 :

If the points P(a, -11), Q(5, b), R(2, 15) and S(1, 1) are the vertices of the parallelogram. Find the value of a and b.

Solution :

For a parallelogram, the midpoint of the diagonals will be equal.

The point of intersection of diagonals will be the in the ratio 1 : 1. PQ and QS are the diagonals of the parallelogram.

= (lx₂ + mx₁) / (l + m), (my₂ + ny₁) / (m + n)

P(a, -11) and R(2, 15)

= 1(2) + 1(a) / (1 + 1), 1(15) + 1(-11) / (1 + 1)

= (2 + a)/2, (15 - 11) / 2

= (2 + a)/2, 4/2

= (2 + a)/2, 2 --------(1)

Q(5, b) and S(1, 1)

= 1(1) + 1(5) / (1 + 1), 1(1) + 1(b) / (1 + 1)

= (1 + 5)/2, (1 + b) / 2

= 6/2, (1 + b)/2

= 3, (1 +b) / 2 --------(2)

(1) = (2)

So, the value of a and b is 4 and 3 respectively.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.