PRACTICAL PROBLEMS USING PARABOLA ELLIPSE AND HYPERBOLA

Question 1 :

A bridge has a parabolic arch that is 10 m high in the centre and 30 m wide at the bottom. Find the height of the arch 6 m from the centre, on either sides.

Solution :

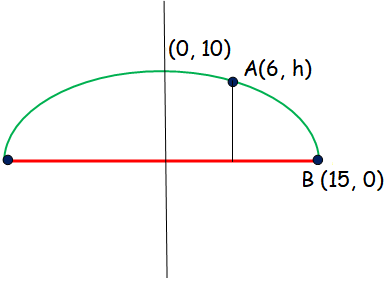
From the given information, the parabola is symmetric about y-axis and it is open down word.

Since the vertex is (h, k),

(x - h)²  =  -4a (y - k)

Here (h, k)  ==>  (0, 10)

(x - 0)²  =  -4a (y - 10)

x²  =  -4a (y - 10)  ----(1)

The parabola is passing through the point (15, 0).

15²  =  -4a (0 - 10)

225/40  =  a

a  =  45/8

By applying the value of a in (1), we get 

x²  =  -4 (45/8) (y - 10)

x²  =  -(45/2) (y - 10)

By applying x = 6 and y = h, we get 

6²  =  -(45/2) (h - 10)

-36(2/45)  =  h - 10

(-72/45) + 10  =  h

h  =  -1.6 + 10

h  =  8.4 m

Hence the required height is 8.4 m.

Question 2 :

A tunnel through a mountain for a four lane highway is to have a elliptical opening. The total width of the highway (not the opening) is to be 16 m, and the height at the edge of the road must be sufficient for a truck 4 m high to clear if the highest point of the opening is to be 5 m approximately . How wide must the opening be?

Solution :

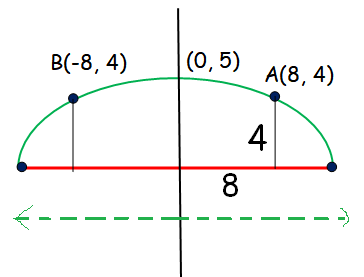
(x²/a²) + (y²/b²)  =  1

The elliptical shape is passing through the point (8, 4).

(8²/a²) + (4²/b²)  =  1

Here b = 5

(8²/a²) + (4²/5²)  =  1

(8²/a²)  =  1 - (16/25)

(64/a²)  =  (25 - 16)/25

(64/a²)  =  9/25

a²  =  64 (25/9)

a  =  8(5)/3

a  =  40/3

2a  =  80/3

2a  =  26.6

Hence the opening must be 26.6 m

Let us look into the next example on "Practical Problems Using Parabola Ellipse and Hyperbola".

Question 3 :

At a water fountain, water attains a maximum height of 4 m at horizontal distance of 0 5 . m from its origin. If the path of water is a parabola, find the height of water at a horizontal distance of 0.75 m from the point of origin.

Solution :

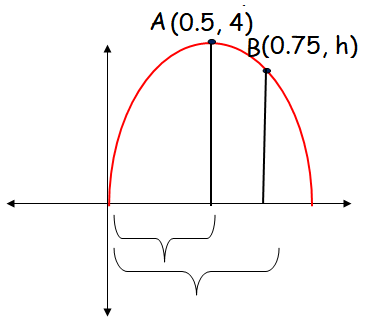
The parabola is symmetric about y-axis and it is open downward.

(x - h)²  =  -4a(y - k)

Te vertex of the parabola is (0.5, 4)

(x - 0.5)²  =  -4a(y - 4) ----(1)

The parabola is passing through the point (0, 0).

(0 - 0.5)²  =  -4a(0 - 4)

0.25  =  16a

a  =  0.25/16

a  =  1/64

By applying the value of a in (1), we get

(x - 0.5)²  =  -4(1/64)(y - 4)

(x - 0.5)²  =  (-1/16)(y - 4)

The parabola is passing through the point (0.75, h), we get

(0.75 - 0.5)²  =  (-1/16)(h - 4)

(0.25)²  =  (-1/16)(h - 4)

-0.0625(16)  =  h - 4

-1 + 4  =  h

h  =  3

Hence the required height is 3 m.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.