PRACTICAL PROBLEMS OF FINDING ANGLES IN STANDARD POSITION
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
|
Angles in quadrants 2nd quadrant 3rd quadrant 4th quadrant |
Formula 180 - given angle 180 + given angle 360 - given angle |
Problem 1 :
A digital protractor is used in woodworking. State the measure of the angle in standard position when the protractor has a reading of 20.4°.

Solution :
To find the angle in standard position, we have to use the formula
180 - given angle
= 180 - 20.4°
= 159.6°
Hence the required angle is 159.6°.
Problem 2 :
Paul and Gail decide to use a Cartesian plane to design a landscape plan for their yard. Each grid mark represents a distance of 10 m. Their home is centered at the origin. There is a red maple tree at the point (3.5, 2). They will plant a flowering dogwood at a point that is a reflection in the y-axis of the position of the red maple. A white pine will be planted so that it is a reflection in the x-axis of the position of the red maple. A river birch will be planted so that it is a reflection in both the x-axis and the y-axis of the position of the red maple.
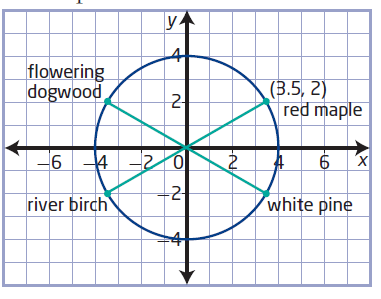
a) Determine the coordinates of the trees that Paul and Gail wish to plant.
b) Determine the angles in standard position if the lines drawn from the house to each of the trees are terminal arms. Express your answers to the nearest degree.
c) What is the actual distance between the red maple and the white pine?
Solution :
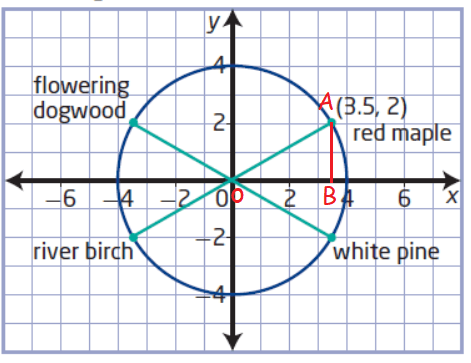
(a) Since the coordinate of flowering dogwood be the reflection of red maple, it will be at (-3.5, 2). The river birch will be at (-3.5, -2) and white pine will be at (3.5, -2).
(b) In triangle OAB,
tan O = AB / OB
tan O = 2/3.5
tan O = 4/7 = 0.571
O = 30°
Hence the red maple will be at 30°.
The angle formed by flowering dogwood is 180 - 30 = 150.
The angle formed by river birch is 180 + 30 = 210.
The angle formed by white pine is 360 - 30 = 330.
c) Distance between the coordinates (3.5, 2) and (3.5, -2).
= √(3.5 - 3.5)2 + (2 + 2)2
= 4 units
Note : Each grid mark represents 10 units.
= 4 units = 4 (10) = 40 m.
Problem 3 :
A windshield wiper has a length of 50 cm. The wiper rotates from its resting position at 30°, in standard position, to 150°. Determine the exact horizontal distance that the tip of the wiper travels in one swipe.
Solution :
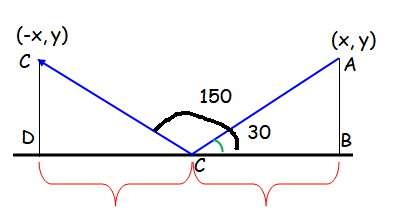
In triangle ACB, we need to find the length of BC.
cos 30 = BC/CA
√3/2 = BC/50
√3(50)/2 = BC
BC = 25√3
BD = 2(BC) = 2(25√3) = 50√3
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 45)
Jan 19, 26 06:14 AM
10 Hard SAT Math Questions (Part - 45) -
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations
