PRACTICAL PROBLEMS INVOLVING MAXIMUM AND MINIMUM VALUES

Problem 1 :

A rectangle has its base on the x axis and its two upper corners on the parabola y = 12-x². What is the largest possible area of the rectangle ?

Solution :

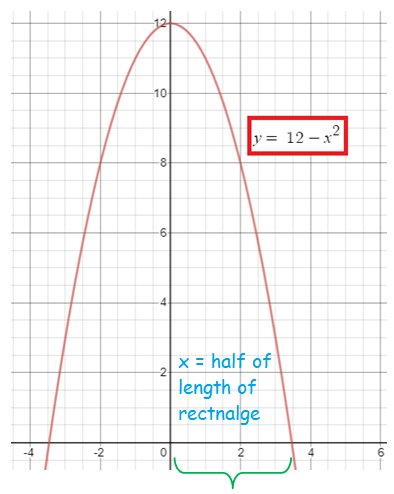
Let x and y be the length and width of the rectangle.

Area of the rectangle  =  length x width

Area of rectangle  =  xy

y = 12-x²

Let us derive equation of area of rectangle in one variable.

A(x)  =  2x (12-x²)

A(x)  =  24x-2x³

A'(x)  =  24(1) - 6x²

A'(x)  =  24 - 6x²

A'(x)  =  0

24 - 6x²  =  0

24  =  6x²

x²  =  4

x  =  2

A''(x)  =  - 6x

When x = 2

A''(2)  =  - 6(2)  ==>  -12 < 0

So, at x = 2, it is maximum.

y  =  12-x²

When x  =  2

y  =  12-2²  ==>  8

The area will be maximum when its dimensions are x  =  2 and y  =  8

Maximum Area  =  A(x)  =  2x(12-x²)

=  2(2) (12-2²)

=  4 (12-4)

=  4 (8)

=  32 square units

So, maximum area is 32 square units.

Problem 2 :

An open rectangular box is to be made from 9 x 12 inch piece of tin by cutting squares of side x inches from the corners and folding up the sides. What should be x be to maximize the volume of the box ?

Solution :

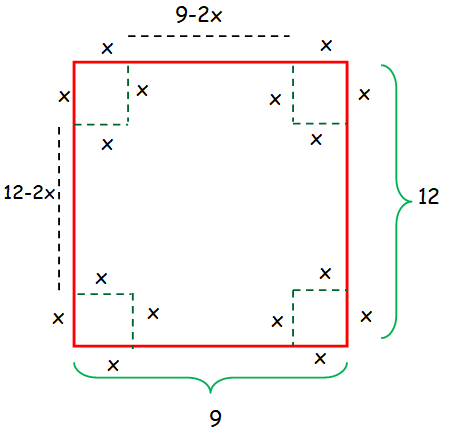
When we fold the rectangular box by cutting the squares at corners, we get the shape cuboid.

Length of cuboid  =  9-2x

Width of cuboid  =  12-2x and

height of cuboid  =  x

Volume of cuboid  =  length ⋅ width ⋅ height

V(x)  =  (9-2x)(12-2x)x

V(x)  =  (9-2x)(12-2x)x

V(x)  =  (9x-2x²)(12-2x)

V(x)  =  108x-42x²+4x³

V'(x)  =  108-84x+12x²

V'(x)  =  0

12x²-84x+108  =  0

x²-7x+9  =  0

Solving this quadratic equation using formula,

(-b±√b²-4ac)/2a

=  (7±√49-36)/2

=  (7±√13)/2

=  (7±3.6)/2

= (7+3.6)/2 or (7-3.6)/2

=  10.6/2 or 3.4/2

x  =  5.3 or 1.7

V'(x)  =  108-84x+12x²

To find at which point it is maximum, we find the second derivative.

V''(x)  =  -84+24x

V''(5.3)  =  -84+24(5.3)

=  -84+127.2

=  43.2 > 0 minimum

V''(x)  =  -84+24x

V''(1.7)  =  -84+24(1.7)

=  -84+40.8

=  -43.2 < 0 maximum

So, the value of x should be 1.7 to maximize the volume.

Problem 3 :

A 384 square meter plot of land is to be enclosed by a fence and divided into two equal parts by another fence parallel to one pair of sides. what dimensions of these outer rectangle will minimize the amount of fence used ?

Solution :

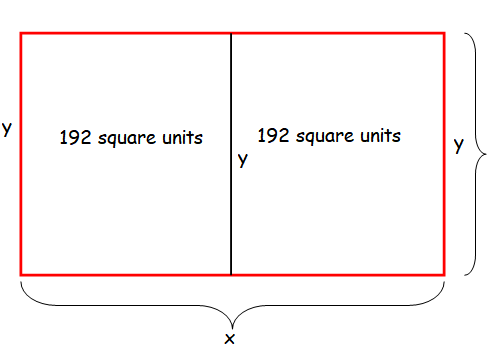
Let x and y be the length and width of the rectangle.

Area of rectangular field  =  384

xy  =  384

y  =  384/x

Perimeter of outer dimension  =  x+y+x+y+y

P  =  2x+3y

Deriving the function in terms of one variable, we get

p(x)  =  2x+3(384/x)

Minimizing the amount of fence  =  Perimeter of field along with the parallel side that we find inside the plot

p'(x)  =  2-3(384/x²)

p'(x)  =  0

2-3(384/x²)  =  0

1152/x²  =  2

x²  =  576

x  =  24

p''(x)  =  6(384/x³)

p''(x)  =  6(384/(24)³) > 0 minimum

When x  =  24, the perimeter is minimum.

y  =  384/24

y  =  16

So, the required dimension is 16 cm x 24 cm.

Problem 4 :

What is the radius of a cylindrical soda can with volume of 512 cubic inches that will use the minimum material ?

Solution :

Volume of the cylindrical can  =  512 cubic inches

πr²h  =  512

To find the material used to make the cylindrical soda can, we should find the total surface area of cylinder.

Total surface area  =  2πr(h+r)  ---(1)

πr²h  =  512 

h  =  512/πr²

By applying the value of h in (1), we get

T(x)  =   2πr(h+r)

T(x)  =   2πr((512/πr²)+r)

T(x)  =   2πr((512+πr³)/πr²)

T(x)  =   2((512+πr³)/r)

T(x)  =  1024/r+2πr²

T'(x)  =  -1024/r²+4πr

T'(x)  =  0

4πr  =  1024/r²

r³  =  512/π

r  =  4.33

T''(x)  =  2048/r³+4π

T''(4.33)  =  2048/(4.33)³+4π  >  0 minimum

So, when r = 4.33 it will take minimum material to be used.

Problem 5 :

A swimmer is at a point 500 m from the closest point on the straight shoreline. She needs to reach a cottage located 1800 m down shore from the closest point. If she swims at 4m/s, she walks at 6 m/s, how far from the cottage should she come ashore so as to arrive at the cottage in the shortest line ?

Solution :

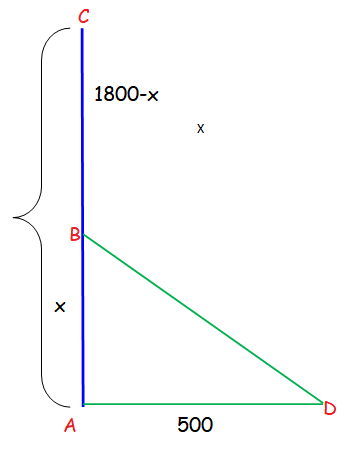
AD is the distance between swimmer and the shore line.

AB  =  From the point D he has to reach B, so the distance between BD

BD²  =  AC² + AD²

BD²  =  x² + 500²

BD  =  √x²+500²

BD is the distance covered by swimming and BC is the distance covered by walk.

Time  =  Distance / Speed

Time taken in swimming(T₁)  =  √(x²+500²)/4

Time taken in walking(T₂)  =  (1800-x)/6

T₁ + T₂  =   √(x²+500²)/4 + (1800-x)/6

T(x)  =  √(x²+500²)/4 + (1800-x)/6

T'(x)  =  2x/8√(x²+500²) - 1/6

T'(x)  =  x/4√(x²+500²) - 1/6

T'(x)  =  0

x/4√(x²+500²)  =  1/6

6x  =  4√(x²+500²)

(3x/2)²  =  (x²+500²)

(9x²-4x²)/4  =  x²+500²

x²  =  (500⋅500⋅4)/5

x  =  200√5

T''(x)  =  [4√(x²+500²) - (x²/√(x²+500²))]/16(x²+500²)

T''(200√5)  >  0

Problem 6 :

Find the closest point on the curve

x²+y²  =  1

to the point (2, 1).

Solution :

Let (x, y) be the required point.

y²  =  1-x² ----(1)

Distance between the point (x, y) and (2, 1).

d  =  √(x-2)²+(y-1)²

f(x)  =  d²  =  (x-2)²+(y-1)²

f(x)  =   (x-2)²+(√(1-x²)-1)²

f(x)  =   x²-4x+4+(1-x²)-2√(1-x²)+1

f(x)  =   -4x+6-2√(1-x²)

f'(x)  =  -4 -(2/2√(1-x²))(-2x)

f'(x)  =  -4 + (2x/√(1-x²))

f'(x)  =  0

(2x/√(1-x²))  =  4

2x  =  4√(1-x²)

4x²  =  16(1-x²)

4x²  =  16-16x²

20x²  =  16

x²  =  16/20

x  =  ±4/2√5

x  =  ±2/√5

So, the closest point on the curve are (2/√5, 1/√5) and (-2/√5, 1/√5) 

Problem 7 :

A window consists of a open rectangle topped by a semicircle and is to have a perimeter of 288 inches. Find the radius of the semicircle that will be maximize the area of the window ?

Solution :

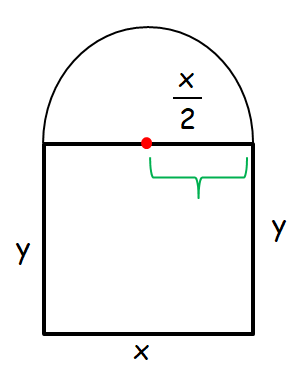
Perimeter  =  288

x + y + y + perimeter of semicircle  =  288

x+2y+π(x/2)  =  288

2y  =  288-x-(πx/2)

y  =  144-(x/2)-(πx/4)

Area  =  x(y) + (1/2)πr²

Area  =  x(144-(x/2)-(πx/4)) + (1/2)π(x/2)²

Area  =  144x-(x²/2)-(πx²/4) + (πx²/8)

Area  =  144x-x²[(1/2)+(π/4)- (π/8)]

A'(x)  =  144-2x[(1/2)+(π/4)- (π/8)]

2x[(1/2)+(π/4)- (π/8)  =  144

2x[(4+2π-π)/8]  =  144

x[(4+π)/4]  =  144

x  =  144(4)/7.14

x  =  80.67

radius  =  x/2  ==>  80.67/2

radius  =  40.3

So, the radius is 40.3.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.