POLYNOMIAL VOCABULARY

Polynomial :

In mathematics, a polynomial is an expression consisting of variables and coefficients, that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables.

Examples :

2x^-1√y - 4 is not a polynomial

3x³ y² is a polynomial in the variable x and y

Terms :

Terms are expressions or numbers that are added or subtracted.

Example :

List out the terms in the following polynomial.

2m² + 5m - 3

Solution :

In the polynomial above, we have three terms.

2m² is the first term

5m is the second term

- 3 is the third term

Degree of a Polynomial :

The degree of a polynomial is the highest exponent or power of the variable that occurs in the polynomial.

Example :

Find the degree of the polynomial

4x³ - 2x² + x - 12

Solution :

The highest power of the given polynomial is 3. Hence the degree of the polynomial is 3.

Leading Term and Leading Coefficient :

The term with the highest degree is called the leading term because it is usually written first. The coefficient of the leading term is called the leading coefficient.

Example :

Find the leading term and leading coefficient in the following polynomial.

3x⁴ - 4x² + x³ + 2x - 7

Solution :

Leading term = 3x⁴

Leading coefficient = 3

Monomial :

We can classify polynomials based on the number of terms. A polynomials which have only one term are known as monomials.

Example :

Find which of the following are monomials

5x - 3 y, 3a, 27m - n + 6, 5x³

Solution :

"3a" and "5x³" are monomials, because they have only one term

Binomial :

We can classify polynomials based on the number of terms. A polynomials which have only two terms are called binomials.

Example :

Find which of the following are binomials

5x - 3 y, 3a - 7 - 5x, 27m - n + 6, 5x³ + 7x

Solution :

"5x - 3 y" and "5x³ + 7x" are binomials, because they have only two terms.

Trinomial :

We can classify polynomials based on the number of terms. A polynomials which have only three terms are called trinomials.

Example :

Find which of the following are trinomials

5x - 3 y, 3a - 7 - 5x, 27m - n + 6, 5x³ + 7x

Solution :

"3a - 7 - 5x" and "27m - n + 6" are tronomials, because they have only three terms. polynomial vocabulary

Constant Polynomial :

We can classify polynomials based on the degree. A polynomial of degree zero is called a constant polynomial.

General form :

p(x) = c, where c is a real number.

Example :

Find which of the following are constant polynomial

5x, 3a, 7, 27m - n + 6

Solution :

"7" is the constant polynomial. polynomial vocabulary

Linear Polynomial :

We can classify polynomials based on the degree. A polynomial of degree one is called a linear polynomial.

General form :

P(x) = ax + b

where a and b are real numbers and "a" is not equal to zero.

Example :

Find which of the following are linear polynomial.

5, 3a, 7 - 5x

Solution :

"7 - 5x" and "3a" are linear polynomials. polynomial vocabulary

Quadratic Polynomial :

We can classify polynomials based on the degree. A polynomial of degree two is called a quadratic polynomial.

General form :

P(x) = ax² + bx + c

where a, b and c are real numbers and "a" is not equal to zero.

Example :

Find which of the following are quadratic polynomials

2m² + 5m - 3, 5a - 3

Solution :

"2m² + 5m - 3" is the quadratic polynomials.

Cubic Polynomial :

We can classify polynomials based on the degree. A polynomial of degree three is called a quadratic polynomial.

General form :

P(x) = ax³ + bx² + cx + d

where a, b, c and d are real numbers and "a" is not equal to zero.

Example :

Find which of the following are cubic polynomials

2m² + 5m - 3

5x³ + 7x

30m³ + 3m² - 163m + 5

Solution :

5x³ + 7x

30m³ + 3m² - 163m + 5

Zero of a Polynomial :

If the value of a polynomial is zero for some value of the variable, then that value of the variable is known as zero of the polynomial.

Example :

Find the zero of the following polynomial.

P(x) = x - 2

Solution :

p(x) = 0

x - 2 = 0

x = 2

The value of the given polynomial becomes zero when the value of x is 2.

So, 2 is the zero of the given polynomial.

Note :

Zero of a polynomial is also called as root.

Adding and Subtracting Polynomials :

To add or subtract polynomials, like terms terms have to be combined.

Example :

Add (7p³ + 4p²- 8p + 1) and (3p³- 5p²- 10p + 5).

Solution :

= (7p³ + 4p²- 8p + 1) + (3p³- 5p²- 10p + 5)

= 7p³ + 4p²- 8p + 1 + 3p³- 5p²- 10p + 5

= 10p³- p²- 18p + 6

Multiplying Polynomials :

To multiply two polynomials, we have to multiply each term in one polynomial by each term in the other polynomial.

Example :

Multiply (x - 2) and (x³ + 2x² - 5) .

Solution :

= (x - 2)(x³ + 2x² - 5)

= (x ⋅ x³) + (x ⋅ 2x²) - (x ⋅ 5) - (2 ⋅ x³) - (2 ⋅ 2x²) + (2 ⋅ 5)

= x⁴ + 2x³ - 5x - 2x³ - 4x² + 10

= x⁴ - 4x² -5x + 10

Dividing Polynomials :

Let p(x) and g(x) be two polynomials such that degree of p(x) > = degree of g(x) and g(x) is not equal to zero.

Then there exists unique polynomials q(x) and r(x) such that

p(x) = g(x) ⋅ q(x) + r(x)

where r(x) = 0 or degree of r(x) < g(x)

Example :

Find the quotient and remainder when (3x²- 4x + 10) is divided by (x - 2).

Solution :

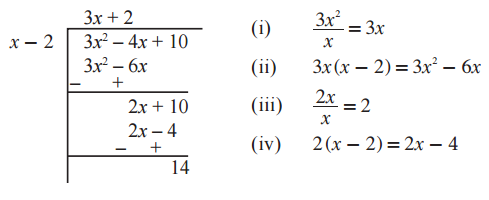
Quotient = 3 x + 2

Remainder = 14

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

POLYNOMIAL VOCABULARY

Recent Articles

Digital SAT Math Problems and Solutions (Part - 176)

Digital SAT Math Problems and Solutions (Part - 179)

Digital SAT Math Problems and Solutions (Part - 178)