POLYNOMIAL FUNCTIONS WORKSHEET FOR GRADE 11

Question 1 :

Find the zeros of the polynomial function f(x) = 4x² − 25.

Question 2 :

If x = −2 is one root of x³ − x² − 17x = 22, then find the other roots of equation.

Question 3 :

Find the real roots of x⁴ = 16.

Question 4 :

Solve (2x + 1)² − (3x + 2)² = 0

Detailed Answer Key

Question 1 :

Find the zeros of the polynomial function f(x) = 4x² − 25.

Solution :

f(x)  =  0

4x² − 25  =  0

4x²  =  25

x²  =  25/4

x  =  √(25/4)

x  =  ±5/2

x  =  5/2 or -5/2

Question 2 :

If x = −2 is one root of x³ − x² − 17x = 22, then find the other roots of equation.

Solution :

Given that : x³ − x² − 17x = 22

 x³ − x² − 17x - 22  =  0

One root of the given polynomial is x  =  -2

From this, we may find the factor (x + 2)

By using synthetic division, we may find other two factors.

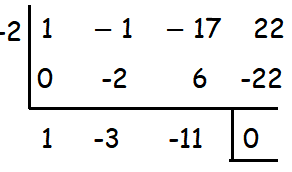
So, the factors are (x + 2) (x² − 3x - 11)

By solving x² − 3x - 11, we may get other two values.

x  =  [-b ± √(b² - 4ac)] / 2a

a  =  1, b = -3 and c = -11

x  =  [3 ± √(3² - 4(1)(-11))] / 2(1)

x  =  [3 ± √(9 + 44)] / 2

x  =  [3 ± √53] / 2

Hence the other roots are (3 + √53)/2 and (3 + √53)/2.

Question 3 :

Find the real roots of x⁴ = 16.

Solution :

x⁴ = 16

x⁴ = 2⁴

x  =  ±2

Question 4 :

Solve (2x + 1)² − (3x + 2)² = 0

Solution :

(2x + 1)² − (3x + 2)² = 0

Expanding the above expression using algebraic identities, we get

(2x + 1) + (3x + 2)  =  0  (or)  (2x + 1) - (3x + 2)  =  0 

Hence the solutions are -3/5 and -1.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.