POLYGONS IN THE COORDINATE PLANE

Example 1 :

Sheila wants to make a pattern of a tile shape with the points A(3, 5), B(4, 6), C(5, 5) and D(4, 4).

What polygon will she get ?

Solution :

Step 1 :

Let us plot the points A(3, 5), B(4, 6), C(5, 5) and D(4, 4) on the coordinate plane. 

Step 2 :

Connect the points in order.

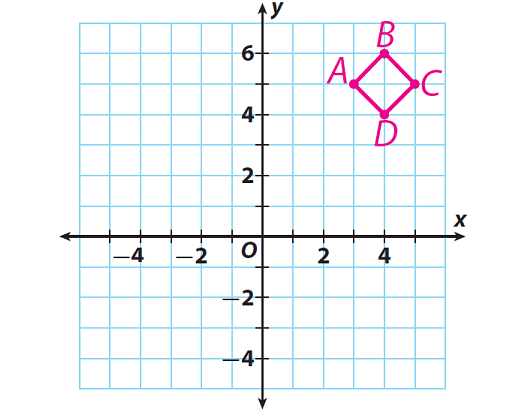
Step 3 :

The polygon formed is a square.

Example 2 :

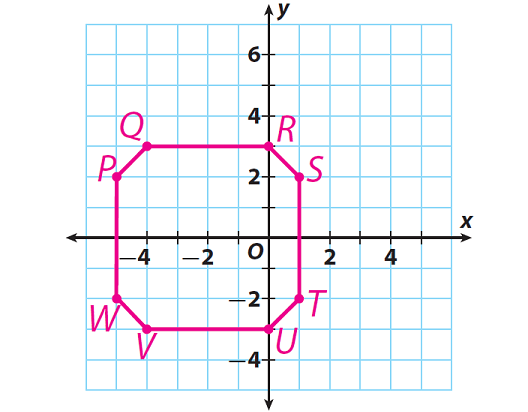
David wants to make a pattern of a tile shape with the points P(-5, 2), Q(-4, 3), R(0, 3), S(1, 2), T(1, -2), U(0, -3), V(-4, -3) and W(-5, -2).

What polygon will he get ?

Solution :

Step 1 :

Let us plot the points P(-5, 2), Q(-4, 3), R(0, 3), S(1, 2),T(1, -2), U(0, -3), V(-4, -3) and W(-5, -2) on the coordinate plane. 

Step 2 :

Connect the points in order.

Step 3 :

The polygon formed is an octagon.

Example 3 :

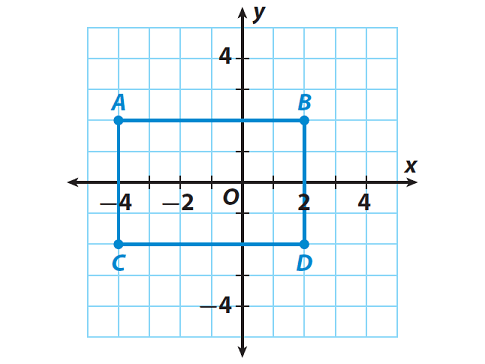
John wants to make a pattern of a tile shape with the points A(-4, 2), B(2, 2), C(2, -2) and D(-4, -2)

What polygon will he get ?

Solution :

Step 1 :

Let us plot the points A(-4, 2), B(2, 2), C(2, -2) and D(-4, -2) on the coordinate plane. 

Step 2 :

Connect the points in order.

Step 3 :

The polygon formed is a rectangle.

Example 4 :

How is the number of vertices related to the number of sides of the polygon and to the type of polygon ? Give two examples.

Solution :

They are the same.

That is, if a polygon has 3 vertices, it would have 3 sides. 

Example :

A polygon with 3 vertices is a triangle and a polygon with 6 vertices is a hexagon.

Example 5 :

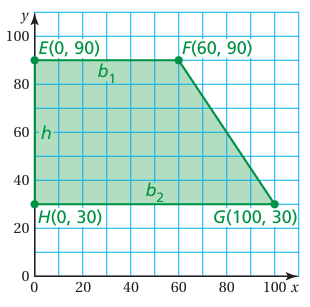
In a grid of the exhibits at a zoo, the vertices of the giraffe exhibit are E (0, 90), F (60, 90), G (100, 30), and H (0, 30). The coordinates are measured in feet. What is the area of the giraffe exhibit?

Solution :

Length of parallel sides,

a = 100 - 0 ==> 100 units

b = 60 - 0 ==> 60 units

Height = 90 - 30

= 60 units

The shape created by the polygon is trapezium.

area of the giraffe exhibit = 1/2 x h x (a + b)

= (1/2) x 60 x (100 + 60)

= 30 x 160

= 4800

The area of the giraffe exhibit is 4800 square feet.

Example 6 :

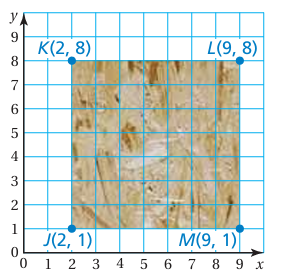
You design a tree house using a coordinate plane. You plot the vertices of the floor at J (2, 1), K (2, 8), L(9, 8), and M (9, 1). The coordinates are measured in feet.

a. What is the shape of the floor?

b. What are the perimeter and the area of the floor?

Solution :

Length of the shape = 9 - 2 ==> 7 units

Width of the shape = 8 - 1 ==> 7 units

a) The shape is square,

b) Perimeter of the shape = 4(7)

= 28 units.

Example 7 :

The vertices of a rectangle are (1, 0), (1, a), (5, a), and (5, 0). The vertices of a parallelogram are (1, 0), (2, b), (6, b), and (5, 0).

The value of a is greater than the value of b. Which polygon has a greater area? Explain your reasoning.

Solution :

(1, 0), (1, a), (5, a), and (5, 0)

By connecting these points, we will get a rectangle.

Di

Length of the rectangle = 5 - 1 ==> 4

Width of the rectangle = a - 0 ==> a

Area of rectangle = 4a square units

(1, 0), (2, b), (6, b), and (5, 0) 

By connecting these points, we will get a parallelogram.

Dimension of parallelogram :

Distance between (1, 0) and (6, b)

Base = 6 - 1

= 5

height = b - 0

= b

Area of parallelogram = 5b

Since a is greater than b, we can conclude that the rectangle has a greater area than the parallelogram. Therefore, the rectangle is the polygon with a greater area.

Example 8 :

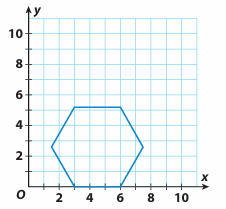
The polygon shown is a regular polygon since all sides have equal length and all angles have equal measure.

a. The polygon is a regular

b. What is the perimeter of the polygon?

Solution :

a) 

Side length of the polygon = 6 - 3

= 3 units

The given shape is hexagon.

b)

Perimeter of hexagon = 6(3)

= 18 units.

Example 9 :

The vertices of a rectangle are F (1, 6), G (7, 6), H (7, 2), and J (1, 2). Draw the rectangle in a coordinate plane and find its perimeter.

Solution :

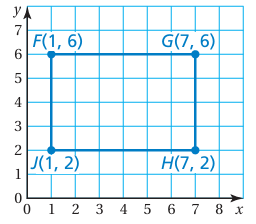
Perimeter of rectangle = 2(length + width)

Length = 7 - 1

= 6 units

Width = 6 - 2

= 4 units

Perimeter = 2(6 + 4)

= 2(10)

= 20 units

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.