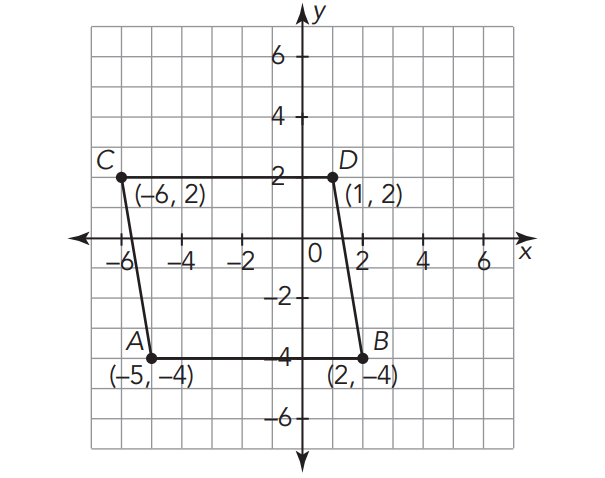
POLYGON ON A COORDINATE PLANE

One advantage of the Cartesian coordinate plane is that it enables mathematicians to use coordinates to analyze geometric figures.

The points in the table above have been graphed on the coordinate plane and connected to form a polygon.

The polygon has opposite sides that are parallel and congruent, so it is a parallelogram. It also has four right angles, so it is a rectangle. The perimeter and area of the rectangle can be calculated by first determining its length and width. The length of the rectangle is 5 units and the width of the rectangle is 4 units.

Perimeter :

4 + 5 + 4 + 5 = 18 units

Area :

5 x 4 = 20 square units

There is often more than one way to complete a polygon on the coordinate plane when given a segment.

For example, on the coordinate plane, the line segment AB is graphed.

Plot and label points C and D to form a parallelogram with a height of 6 units.

Two different examples of Parallelogram ABCD are shown. Each has a length of 7 units and height of 6 units, so they both have an area of

7 x 6 = 42 square units

The distance between two points on a coordinate plane can be calculated by using the coordinates of the two points.

For example, the design of a playground is laid out in a grid with a unit of 1 foot. The coordinates of the sand pit that will go under the swing set are located at

(-15, 7), (-10, 7), (-15, 21), and (-10, 21)

Determine the volume of the sand pit if the pit is 0.5 foot deep.

Plotting the coordinates of the sand pit on a coordinate plane shows that the shape of the sand pit is a rectangle. Use the coordinates to determine the distance between the points which will give you the length and width of the rectangle.

Width :

|- 15| - |-10| = 15 - 10 = 5 feet

Length :

|7| + |-1| = 7 + 1 = 8 feet

Area :

8 x 5 = 40 square feet

Volume :

8 x 5 x 0.5 = 20 cubic feet

Find the area of composite figure :

Problem 1 :

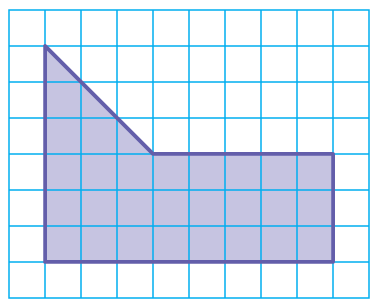
Solution :

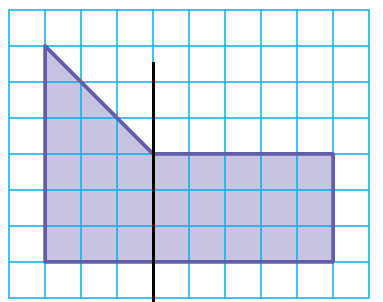
Area of the shape = Area of trapezium + area of rectangle

Area of trapezium = 1/2 x h x (a + b)

Area of rectangle = length x width

height = 3, a = 6 and b = 3

length = 5, width = 3

= (1/2) x 3 x (6 + 3) + 5 x 3

= 1.5 x 9 + 15

= 13.5 + 15

= 28.5 square units

Area of the shape given = 28.5 square units

Problem 2 :

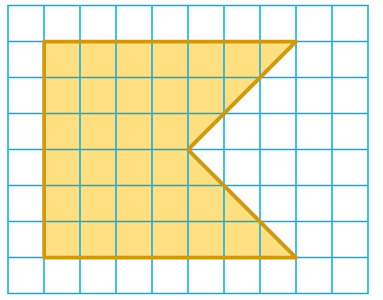
Solution :

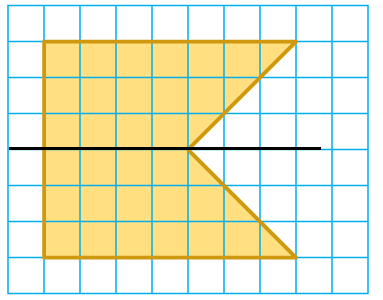
Area of the shape = 2 x area of trapezium

Let a and b be parallel sides and h be the height

a = 7, b = 4, h = 3

Area of trapezium = (1/2) x h (a + b)

Area of shape = 2 x (1/2) x 3 x (7 + 4)

= 3 x 11

= 33 square feet

Area of the shape given = 33 square feet

Problem 3 :

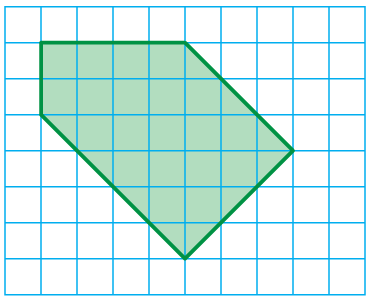
Solution :

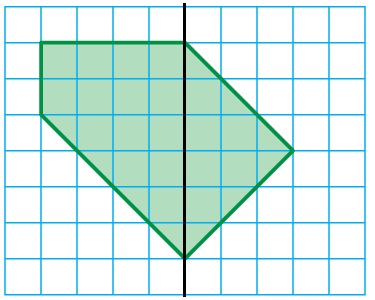
Area of the shpae in the coordinate plane

= area of triangle + area of trapezium

= (1/2) x 6 x 3 + (1/2) x 4 x (2 + 6)

= 3 x 3 + 2 x 8

= 9 + 16

= 25 square units.

Area of the shape given = 25 square units.

Problem 4 :

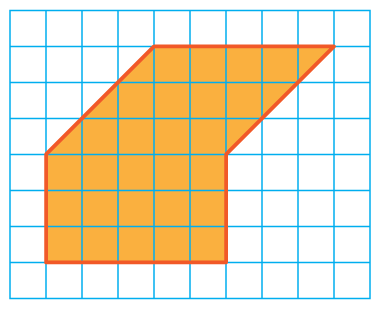
Solution :

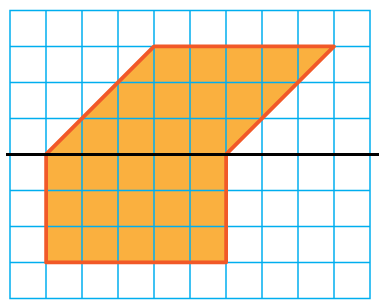
Area of the shape

= area of rectangle + area of parallelogram

length = 5, width = 3

height of parallelogram = 3, base = 5

Area of rectangle = length x width

Area of parallelogram = base x height

= 5 x 3 + 5 x 3

= 15 + 15

= 30 square units.

Area of the shape given = 30 square units

Problem 5 :

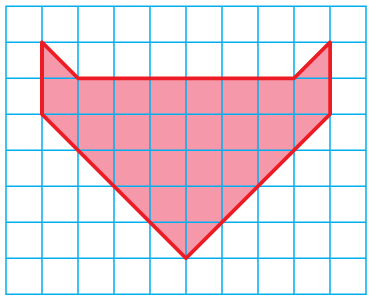
Solution :

Area of shape

= 2 area of trapezium + area of rectangle + area of triangle

= 2 x (1/2) x (2 + 1) x 1 + 6 x 1 + (1/2) x 8 x 4

= 3 + 6 + 16

= 25 square units.

Area of the shape given = 25 square units

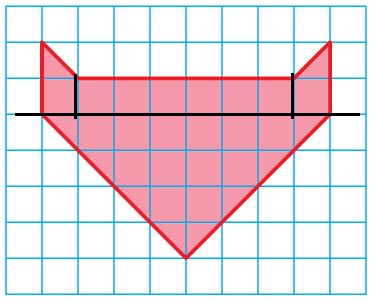
Problem 6 :

Solution :

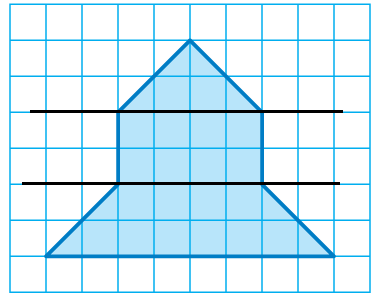
Area of shape = area of triangle + area of rectangle + area of trapezium

base = 4, height = 2

length = 4, width = 2

a = 8, b = 4, h = 2

= (1/2) x 4 x 2 + 4 x 2 + (1/2) x 2 (8 + 4)

= 4 + 8 + 12

= 24 square units.

Area of the shape given = 24 square units.

Problem 7 :

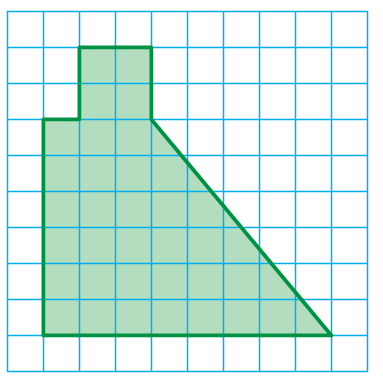
Solution :

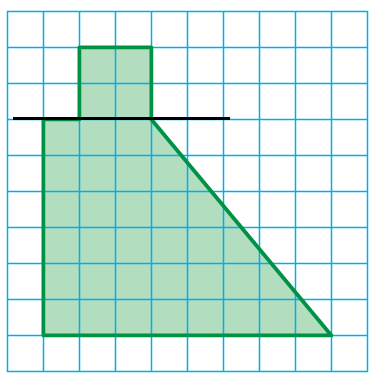
Area of shape given = aera of square + area of trapezium

= 2 x 2 + (1/2) x 6 x (8 + 3)

= 4 + 3 x 11

= 4 + 33

= 37 square units

So, the area of the shape given is 7 square units.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.