POINTS LINES AND PLANES

In geometry, some words, such as point line and plane are undefined terms. Although these words are formally defined, it is important to have general agreement about what each word means.

Point :

A point has no dimension and it is usually represented by a small dot.

Line :

A line extends in one dimension. It is usually represented by a straight line with two arrowheads to indicate that the line extends without end in two directions.

Plane :

A plane extends in two dimensions. It is usually represented by a shape that looks like a tabletop or wall. We have to imagine that the plane extends without end, even though the drawing of a plane appears to have edges.

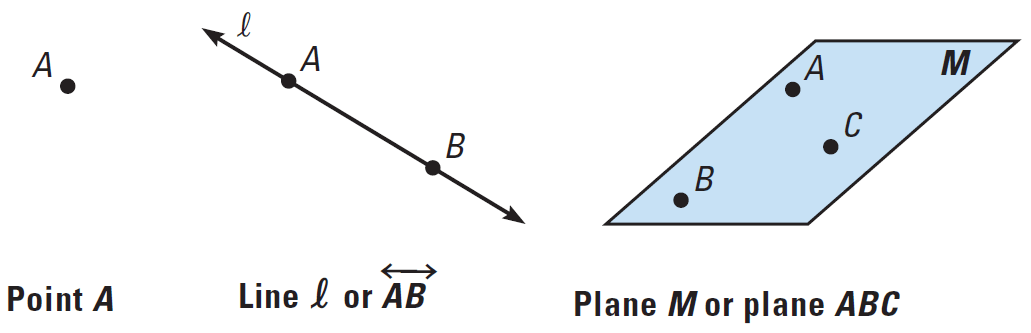
A few basic concepts in geometry must also be commonly understood without being defined. One such concept is the idea that a point lies on a line or a plane.

Collinear points are the points which lie on the same line.

Coplanar points are the points which lie on the same plane.

Example 1 :

Look at the figure given below and answer the questions.

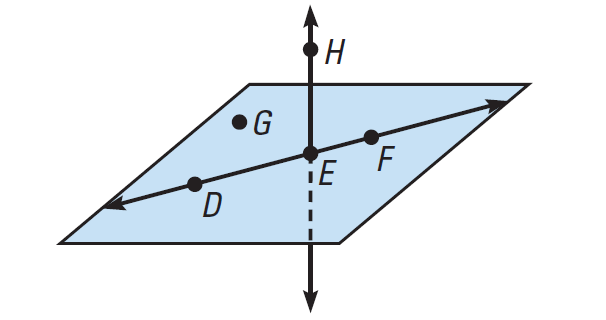
(i) Name three points that are collinear.

(ii) name four points that are coplanar.

(iii) Name three points that are not collinear.

Solution :

Solution (i) :

Points D, E and F lie on the same line. So they are collinear.

Solution (ii) :

Points D, E, F and G lie on the same plane. So they are coplanar. D, E, F and H are coplanar, even though the plane containing them is not drawn.

Solution (iii) :

There are many correct answers. For instance, points H, E and G do not lie on the same line.

Example 2 :

Draw three non collinear points, J, K and L. Then draw the lines JK, KL and LJ.

Solution :

Step 1 :

Draw the points J, K and L as given below.

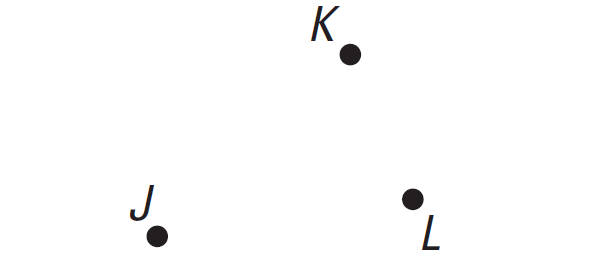
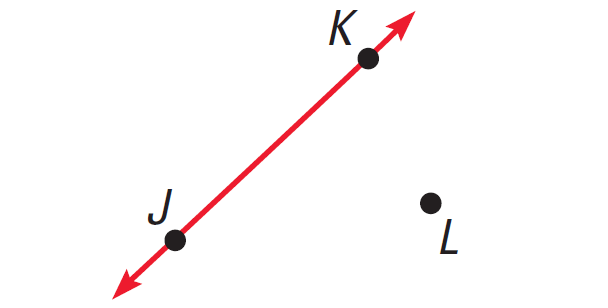
Step 2 :

Draw the line JK by connecting the points J and K as given below.

Step 3 :

Draw the line KL by connecting the points K and L as given below.

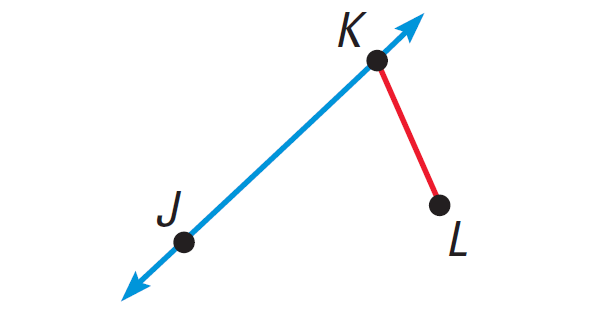
Step 4 :

Draw the line LJ by connecting the points L and J as given below.

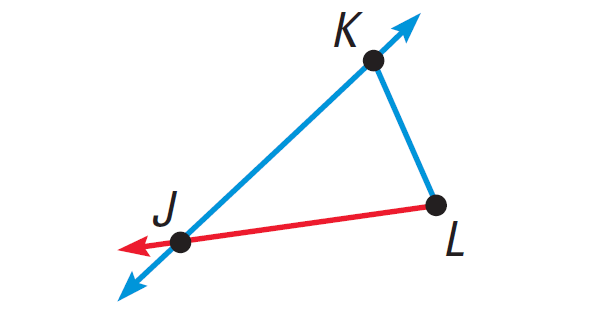
Example 3 :

Draw two lines, label points on the lines and name two pairs of opposite rays.

Solution :

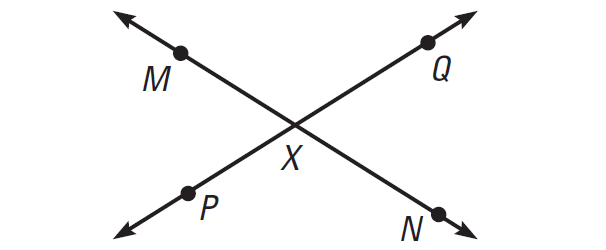
Points M, N and X are collinear and X is between M and N.

So, XM and XN are opposite rays.

Points P, Q and X are collinear and X is between P and Q.

So, XP and XQ are opposite rays.

Example 4 :

Sketch the figure described.

"A line that intersects a plane in one point"

Solution :

(i) Draw a plane and a line.

(ii) Mark the point where they meet.

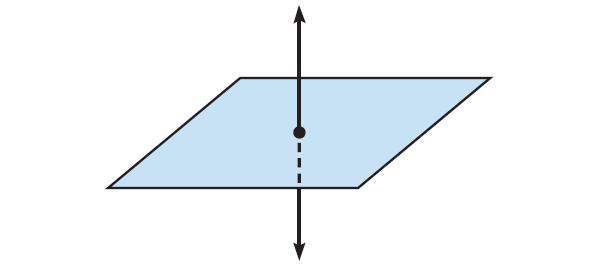
Dashes indicate where the line is hidden by the plane.

Example 5 :

Sketch the figure described.

"Two planes that intersect in a line"

Solution :

(i) Draw two planes.

(ii) Mark the line where they meet.

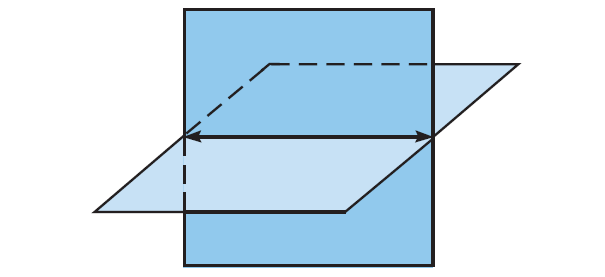
Dashes indicate where one plane is hidden by the other plane.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.