POINT SLOPE FORM

If you know the slope and any point on the line, you can write an equation of the line by using the slope formula. For example, suppose a line has a slope of 2 and contains (3, 5) . Let (x, y) be any other point on the line.

Slope Formula : 

m  =  (y₂ - y₁)/(x₂ - x₁)

Substitute m = 2, (x₁, y₁) = (3, 5) and (x₂, y₂) = (x, y). 

2  =  (y - 5)/(x - 3)

Multiply each side by (x - 3). 

2(x - 3)  =  y - 5

or

y - 5  =  2(x - 3)

Point-Slope Form of a Linear Equation

The line with slope 'm' that contains the point (x₁ , y₁) can be described by the equation

y - y₁  =  m(x - x₁)

Writing Linear Equations in Point-Slope Form

Write an equation in point-slope form for the line with the given slope that contains the given point.

Example 1 :

Slope = 5 ; (2, 0).

Solution :

Write the point-slope form.

y - y₁  =  m(x - x₁)

Substitute 5 for m, 2 for x₁ and 0 for y₁.  

y - 0  =  5(x - 2)

Example 2 :

Slope = -7 ; (-2, 3).

Solution :

Write the point-slope form.

y - y₁  =  m(x - x₁)

Substitute -7 for m, -2 for x₁ and 3 for y₁.  

y - 3  =  -7[x - (-2)]

y - 3  =  -7(x + 2)

Using Point-Slope Form to Graph

Graph the line described by each equation.

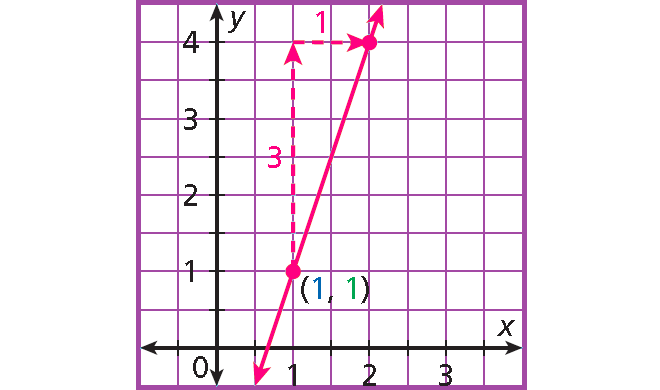
Example 3 :

y - 1  =  3(x - 1)

Solution :

y - 1 = 3 (x - 1) is in the form y - y₁ = m(x - x₁).

Slope m = 3 = 3/1

The line contains the point (1, 1) .

Step 1 : 

Plot (1, 1).

Step 2 : 

Count 3 units up and 1 unit right and plot another point.

Step 3 : 

Draw the line connecting the two points.

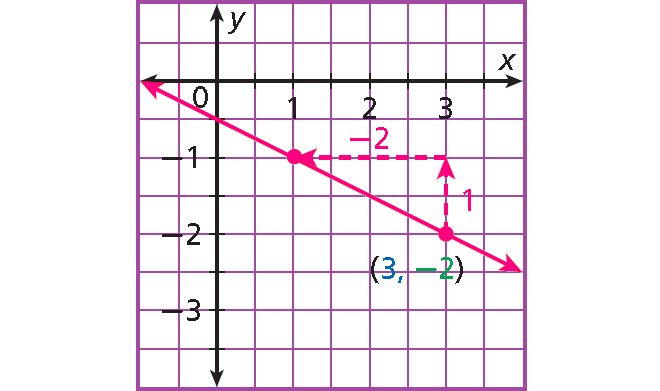
Example 4 :

y + 2  =  (-1/2)(x - 3)

Solution :

Step 1 : 

Write the equation in point-slope form :

y - y₁  =  m(x - x₁)

y + 2  =  (-1/2)(x - 3)

Rewrite addition of 2 as subtraction of -2.

y - (-2)  =  (-1/2)(x - 3)

Step 2 : 

The line contains the point (3, -2).

Slope m = -1/2 = 1/(-2)

• Plot (3, -2). 
• Count 1 unit up and 2 units left and plot another point.
• Draw the line connecting the two points.

Writing Linear Equations in Slope-Intercept Form

Write the equation that describes each line in slope-intercept form.

Example 5 :

slope = -4, (-1, -2) is on the line.

Solution :

Because the slope of the line and a point on the line are given, we can write the equation of the line in point-slope form.

y - y₁  =  m(x - x₁)

Substitute m = -4 and (x₁, y₁) = (-1, -2).

y - (-2)  =  -4[x - (-1)]

Simplify and solve for y : 

y + 2  =  -4(x + 1)

Distribute -4 on the right side.

y + 2  =  -4x - 4

Subtract 2 from each side.

y + 2  =  -4x - 4

y  =  -4x - 6

Example 6 :

(1, -4) and (3, 2) are on the line.

Solution :

Find the slope.   

m  =  (y₂ - y₁)/(x₂ - x₁)

=  [2 - (-4)]/(3 - 1)

=  (2 + 4)/2

=  6/2

=  3

Substitute the slope and one of the points into the point-slope form. Then write the equation in slope-intercept form.

y - y₁  =  m(x - x₁)

Substitute m = 3, (x₁, y₁) = (3, 2). 

y - 2  =  3(x - 3)

Simplify. 

y - 2  =  3x - 9

Add 2 to each side.

y  =  3x - 7

Example 7 :

x-intercept = –2, y-intercept = 4.

Solution :

Use the intercepts to find two points :

(-2, 0) and (0, 4)

Find the slope. 

m  =  (y₂ - y₁)/(x₂ - x₁)

=  (4 - 0)/[(0 -(-2)]

=  4/2

=  2

Write the equation in slope-intercept form.

y  =  mx + b

Substitute 2 for m and 4 for b.

y  =  2x + 4

Using Two Points to Find Intercepts

Example 8 :

The points (4, 8) and (-1, -12) are on a line. Find the intercepts.

Solution :

Step 1 :

Find the slope. 

m  =  (y₂ - y₁)/(x₂ - x₁)

=  (-12 - 8)/(-1 - 4)

=  -20/(-5)

=  4

Step 2 :

Write the equation in point-slope form.

y - y₁  =  m(x - x₁)

Substitute m = 4, (x₁, y₁) = (4, 8). 

y - 8  =  4(x - 4)

Simplify and solve for y. 

y - 8  =  4x - 16

Add 8 to each side.

y  =  4x - 8

Step 3 :

Find the intercepts : 

The x-intercept is 2, and the y-intercept is -8.

Problem-Solving Application

Example 9 : 

The cost to place an ad in a newspaper for one week is a linear function of the number of lines in the ad. The costs for 3, 5, and 10 lines are shown. Write an equation in slope-intercept form that represents the function. Then find the cost of an ad that is 18 lines long.

Solution :

Understand the Problem :

• The answer will have two parts—an equation in slope-intercept form and the cost of an ad that is 18 lines long.

• The ordered pairs given in the table satisfy the equation.

Make a Plan :

First, find the slope. Then use point-slope form to write the equation. Finally, write the equation in slope-intercept form.

Solve :

First, find the slope. Then use point-slope form to write the equation. Finally, write the equation in slope-intercept form.

Step 1 :

Choose any two ordered pairs from the table to find the slope.

m = (y₂ - y₁)/(x₂ - x₁)

Use (3, 13.50) and (5, 18.50).

=  (18.50 - 13.50)/(5 - 3)

=  5/2

=  2.5

Step 2 :

Substitute the slope and any ordered pair from the table into the point-slope form.

y - y₁  =  m(x - x₁)

Substitute m = 2.5, (x₁, y₁) = (10, 31). 

y - 31  =  2.5(x - 10)

Step 3 :

Write the equation in slope-intercept form by solving for y.

y - 31  =  2.5(x - 10)

Distribute 2.5.

y - 31  =  2.5x - 25

Add 31 to each side. 

y  =  2.5x + 6

Step 4 :

Find the cost of an ad containing 18 lines by substituting 18 for x.

y  =  2.5x + 6

y  =  2.5(18) + 6

y  =  45 + 6

y  =  51

The cost of an ad containing 18 lines is $51.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.