POINT SLOPE FORM EQUATION OF A LINE WORKSHEET

1. Find the point-slope form equation of line passing through the point (1, 2) with slope -4.

2. Find the equation of line in slope-intercept form which is passing through the point (-2, 3) with slope 3.

3. Find the equation of line in general form which is passing through the point (-5, -4) with slope 2/3.

4. Find the equation of a line in standard passing through the point (3, -4) and having slope -5.

5. Find the point-slope form equation of the straight line passing through the point (1, 2) and parallel to the line whose equation is x + 2y + 3 = 0.

6. Find the point-slope form equation of the straight line passing through the point (-2, 3) and perpendicular to the line whose equation is x - 2y - 6 = 0.

7. Find the equation of line in point-slope form which passing through the point (1, 4) and perpendicular to the line joining points (2, 5) and (4, 7).

1. Answer :

Given : Point = (1, 2) and slope m = -4.

Equation of line in point-slope form :

y - y₁ = m(x - x₁)

Substitute (x₁ , y₁) = (1 , 2) and m = -4.

y - 2 = -4(x - 1)

2. Answer :

Given : Point = (-2, 3) and slope m = 3.

Equation of line in point-slope form :

y - y₁ = m(x - x₁)

Substitute (x₁ , y₁) = (-2 , 3) and m = 3.

y - 3 = 3[x - (-2)]

y - 3 = 3(x + 2)

y - 3 = 3x + 6

Hence, the equation of line in slope-intercept form :

y = 3x + 9

3. Answer :

Given : Point = (-5, -4) and slope m = 2/3.

Equation of line in point-slope form :

y - y₁ = m(x - x₁)

Substitute (x₁ , y₁) = (-5 , -4) and m = 2/3.

y - (-4) = (-2/3)[x - (-5)]

y + 4 = (-2/3)(x + 5)

3(y + 4) = -2(x + 5)

3y + 12 = -2x - 10

Hence, the equation of line in general form :

2x + 3y + 22 = 0

4. Answer :

Given : Point = (3, -4) and slope m = -5.

Equation of line in point-slope form :

y - y₁ = m(x - x₁)

Substitute (x₁ , y₁) = (3 , -4) and m = -5.

y - (-4) = -5(x - 3)

y + 4 = -5x + 15

Hence, the equation of line in standard form :

5x + y = 11

5. Answer :

Write the equation of the line 'x + 2y + 3 = 0' in slope intercept form.

x + 2y + 3 = 0

2y = -x - 3

y = (-1/2)x - 3/2

Slope of the given line is -1/2.

Because the required line is parallel to the given line, the slopes are equal.

Then, slope of the required line is -1/2.

The required line is passing through (1, 2) with slope -1/2.

Equation of line in point-slope form :

y - y₁ = m(x - x₁)

Substitute (x₁ , y₁) = (1, 2) and m = -1/2.

y - 2 = (-1/2)(x - 1)

6. Answer :

Write the equation of the line 'x - 2y - 6 = 0' in slope intercept form.

x - 2y - 6 = 0

-2y = -x + 6

2y = x - 6

y = (1/2)x - 3

Slope of the given line is 1/2.

Because the required line is perpendicular to the given line, product of the slopes is equal to -1.

Let 'm' be the slope of the required line.

m x (1/2) = -1

m/2 = -1

m = -2

The required line is passing through (-2, 3) with slope -2.

Equation of line in point-slope form :

y - y₁ = m(x - x₁)

Substitute (x₁ , y₁) = (-2, 3) and m = -2.

y - 3 = -2[x - (-2)]

7. Answer :

Let the given points be A(1, 4), B(2, 5) and C(4, 7).

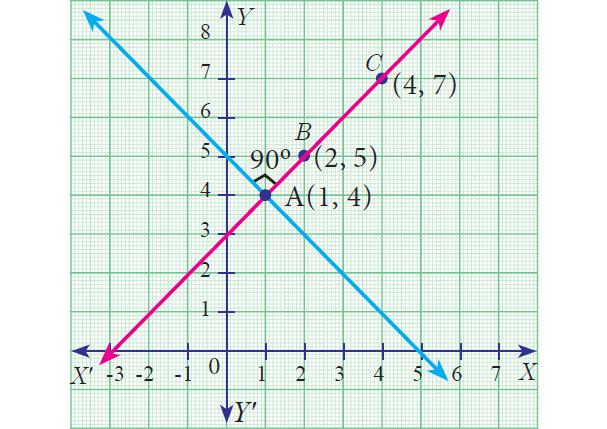
Slope of line BC = (7 - 5)/(4 - 2)

= 2/2

= 1

Let m be the slope of the required line.

Since the required line is perpendicular to BC,

m x 1 = -1

m = -1

The required line is passing through A(1, 4) with slope -1.

Equation of line in point-slope form :

y - y₁ = m(x - x₁)

Substitute (x₁ , y₁) = (1, 4) and m = -1.

y - 4 = -1(x - 1)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.