PLOTTING A POINT IN THE PLANE IF ITS COORDINATES ARE GIVEN
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
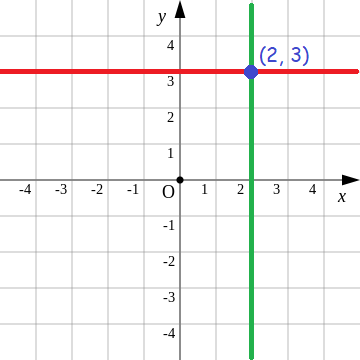
Plot the point (2, 3) in a xy-plane.
Solution :
In the given point (2, 3),
x-coordinate = 2
y-coordinate = 3
Draw a vertical line through the value 2 on x-axis and horizontal line through the value 3 on y-axis. The point of intersection of the vertical line and horizontal line is the location of (2, 3).
Problem 2 :
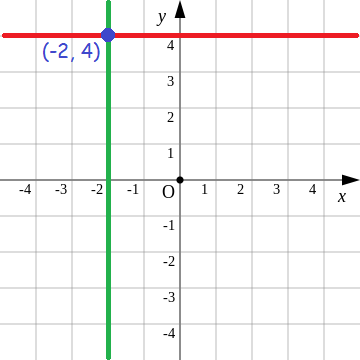
Plot the point (-2, 4) in a xy-plane.
Solution :
In the given point (-2, 4),
x-coordinate = -2
y-coordinate = 4
Draw a vertical line through the value -2 on x-axis and horizontal line through the value 4 on y-axis. The point of intersection of the vertical line and horizontal line is the location of (-2, 4).
Problem 3 :
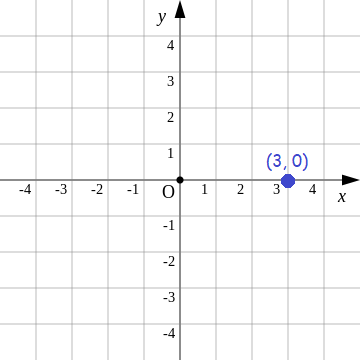
Plot the point (3, 0) in a xy-plane.
Solution :
In the given point (3, 0),
x-coordinate = 3
y-coordinate = 0
Since the y-coordinate of the given point is zero, it lies on the x-axis at 3.
Problem 4 :
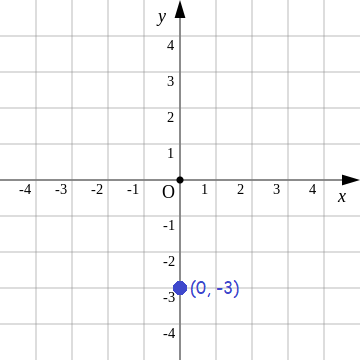
Plot the point (0, -3) in a xy-plane.
Solution :
In the given point (0, -3),
x-coordinate = 0
y-coordinate = -3
Since the x-coordinate of the given point is zero, it lies on the y-axis at -3.
Problem 5 :
Find the distance between the points (-2, 3) and (4, 3) in a xy-plane.
Solution :
Plot the points (-2, 3) and (5, 3) in a xy-plane measure the distance between them.
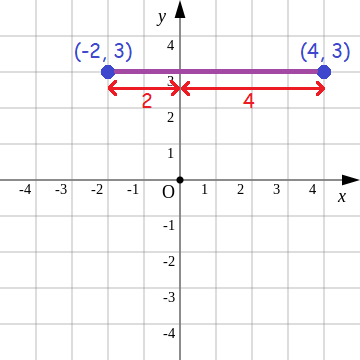
The distance between the points (-2, 3) and (4, 3) :
= 2 + 4
= 6 units
Problem 6 :
Find the distance between the points (3, -2) and (3, 4) in a xy-plane.
Solution :
Plot the points (3, -2) and (3, 4) in a xy-plane measure the distance between them.
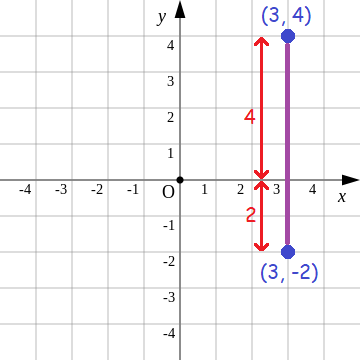
The distance between the points (3, -2) and (3, 4) :
= 2 + 4
= 6 units
Problem 7 :
Find the distance between the points (0, 4) and (3, 0) in a xy-plane.
Solution :
Plot the points (0, 4) and (3, 0) in a xy-plane measure the distance between them.
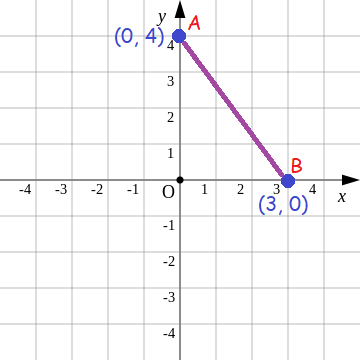
Here, the distance between the points (0, 4) and (3, 0) is neither horizontal nor vertical.
So, we can consider the right triangle OAB. We have right angle at O and AB is the hypotenuse.
Using Pythagorean Theorem,
AB2 = OA2 + OB2
AB2 = 42 + 32
AB2 = 16 + 9
AB2 = 25
Taking square root on both sides,
AB = 5
The distance between the points (0, 4) and (3, 0) is 5 units.
Problem 8 :
Find the distance of the point (3, 2) from y-axis.
Solution :
Plot the points (3, 2) and measure the distance from y-axis.
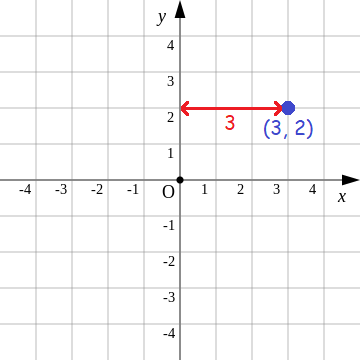
The distance of the point (3, 2) from y-axis is 3 units.
Problem 9 :
Find the distance of the point (-2, -4) from x-axis.
Solution :
Plot the points (-2, -4) and measure the distance from x-axis.
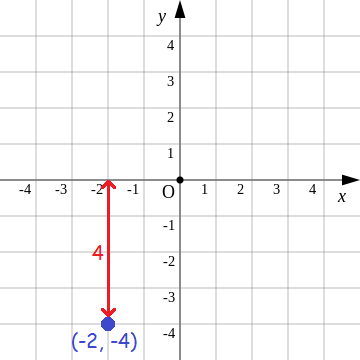
The distance of the point (-2, -4) from x-axis is 4 units.
Problem 10 :
In a xy-plane, Chloe is located at (1, -1). Paul is located 3 units to the north and 4 units to the west of Chloe's location. Find Paul's location.
Solution :
Plot the points (1, -1). Then, move 3 units to the north and 4 units to the west to find Paul's location.
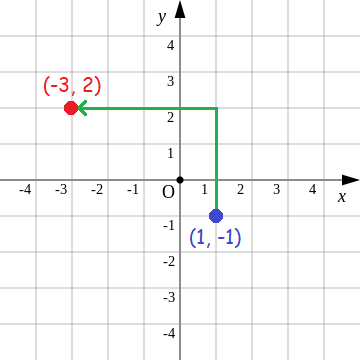
Paul's location is (-3, 2).
Problem 11 :
In a xy-plane, Abraham is located at (-3, -1). Lincoln is located 4 units to the north and 6 units to the east of Abraham's location. Find Lincoln's location.
Solution :
Plot the points (-3, -1). Then, move 4 units to the north and 6 units to the east to find Lincoln's location.
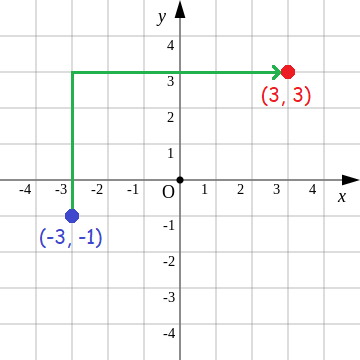
Lincoln's location is (3, 3).
Problem 12 :
In a xy-plane, Lily is located at (-2, 3). Andrea is located 5 units to the south, 4 units to the east and 3 units to the north of Lily's location. Find Andrea's location.
Solution :
Plot the points (-2, 3). Then, move 5 units to the north, 4 units to the east and 3 units to the north to find Andrea's location.
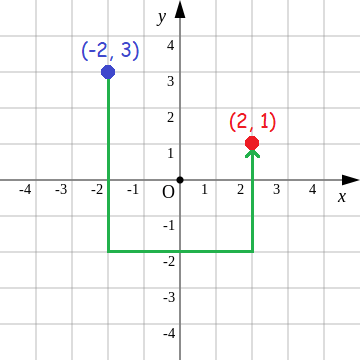
Andrea's location is (2, 1).
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4)
