PLACE VALUE AND FACE VALUE

Place Value :

Place value of a digit in a number is the digit multiplied by thousand or hundred or whatever place it is situated.

Example :

In 25486, the place value of 5 is

= 5 ⋅ 1000

= 5000

Here, to get the place value of 5, we multiply 5 by 1000.

Because 5 is at thousands place.

Face Value :

Face value of a digit in a number is the digit itself.

More clearly, face value of a digit always remains same irrespective of the position where it is located.

Example :

In 25486, the face value of 5 is 5.

Difference between Place Value and Face Value

The difference between place value and face value has been illustrated in the picture given below.

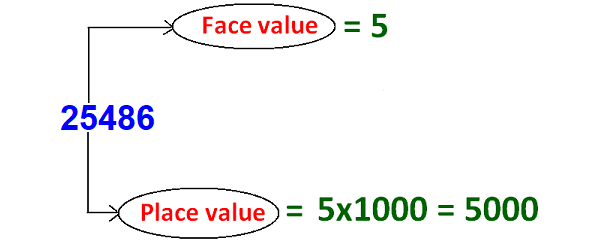
Place Value

For better understanding, here  we are going to discuss about place value in detail.

When we look at the picture given below, we can clearly understand place value.

To have better understanding of the picture, let us consider an example.

Find the place value of the digit 5 in the number 25486.

Solution :

As per the first branch, the location of 5 in 25486 is thousands place.

As per the second branch, the value of 5 in 25486 is 5000.

Finally, the place value of 5 in 25486 is 5000.

Finding Place Value - Shortcut

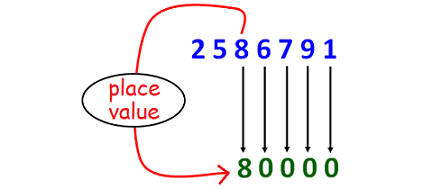
Finding Place Value - Steps

Problem 1 :

Find the face value and place value of the underlined digit in the number given below.

253869

Solution :

In the number above, 6 is underlined.

The face value of 6 is the same.

So, the face value of 6 is 6.

To get place value, we have to count the number of digits after 6.

There is only one digit after 6.

So, the place value of 6 is 60.

Problem 2 :

Find the face value and place value of the underlined digit in the number given below.

563472

Solution :

In the number above, 2 is underlined.

The face value of 2 is the same. 

So, the face value of 2 is 2.

To get place value, we have to count the number of digits after 2.

There is no more digit after 2.

So, the place value of 2 is 2.

Problem 3 :

Find the place value of K in the number given below.

K78952

Given that K = 2x and x = 3.

Solution :

From the given information, let us find the value of K.

K = 2x = 2(3) = 6 ----> K = 6

So, we have

K78952 ----> 678952

To get place value of K, we have to count the number of digits after 6.

There are five digits after 6.

So, the place value of K is 600000.

Problem 4 :

Find the place value of K in the number given below.  Given that K is the even prime number.

78K346

Solution :

From the given information, let us find the value of K.

K = 2

(Because 2 is the only even prime number we have in math)

So, we have

78K346 ----> 782346

To get place value of K, we have to count the number of digits after 2.

There are three digits after 2.

So, the place value of K is 2000.

Problem 5 :

Find the place value of K in the number given below.  Given that K is a number which is less than 10 and exactly divisible by both 2 and 3.

32K58

Solution :

From the given information, let us find the value of K.

K = 6

(Because 6 is the only number less than 10 and also exactly divisible by both 2 and 3)

So, we have

32K58 ----> 32658

To get place value of K, we have to count the number of digits after 6.

There are two digits after 6.

So, the place value of K is 200.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.