PERPENDICULARS AND BISECTORS

Perpendicular :

Perpendicular is a segment, ray, line, or plane that intersects another segment at right angle.

Bisector :

Bisector is a segment, ray, line, or plane that intersects another segment at its midpoint.

Perpendicular Bisector :

A segment, ray, line, or plane that is perpendicular to another segment at its midpoint is called a perpendicular bisector.

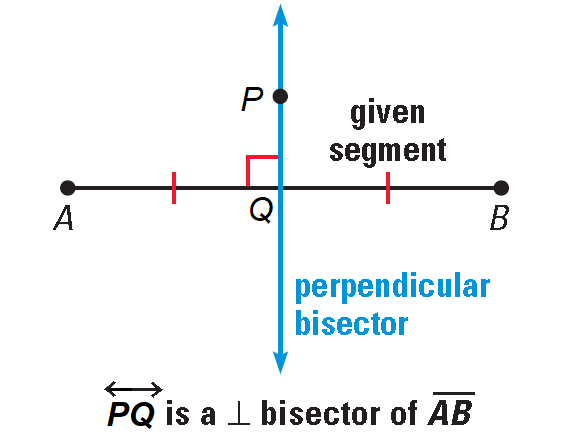
Construction of Perpendicular Through a Point on a Line

To construct a perpendicular bisector of a line segment, you must need the following instruments.

1. Ruler

2. Compass

The steps for the construction of a perpendicular bisector of a line segment are :

Step 1 :

Draw the line segment AB.

Step 2 :

With the two end points A and B of the line segment as centers and more than half the length of the line segment as radius draw arcs to intersect on both sides of the line segment at C and D.

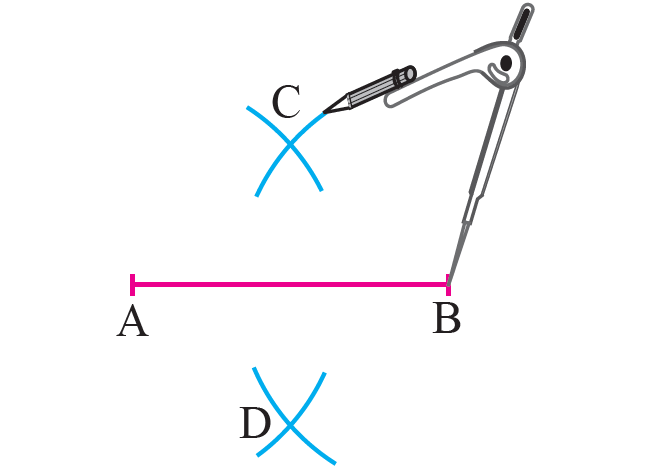
Step 3 :

Join C and D to get the perpendicular bisector of the given line segment AB.

In the above figure, CD is the perpendicular bisector of the line segment AB.

This construction clearly shows how to draw the perpendicular bisector of a given line segment with compass and straightedge or ruler. This bisects the line segment (That is, dividing it into two equal parts) and also perpendicular to it. Since this bisects, it finds the midpoint of the given line segment.

Perpendicular Bisector Theorem

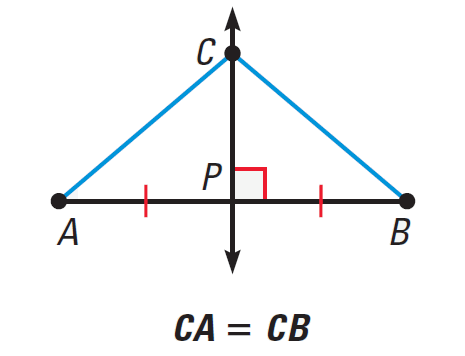
If a point is on the perpendicular bisector of a segment, then it is equidistant from the endpoints of the segment. 

If CP is the perpendicular bisector AB, then

CA = CB

It has been illustrated in the diagram shown below.

Converse of the Perpendicular Bisector Theorem

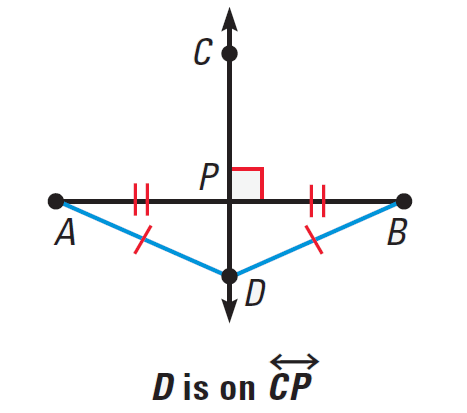
If a point is equidistant from the endpoints of a segment, then it is on the perpendicular bisector of the segment.

If DA = DB, then D lies on the perpendicular bisector of AB.

It has been illustrated in the diagram shown below.

Angle Bisector Theorem

If a point is on the bisector of an angle, the it is equidistant from the two sides of the angle.

If m∠BAD = m∠CAD, then

DB = DC

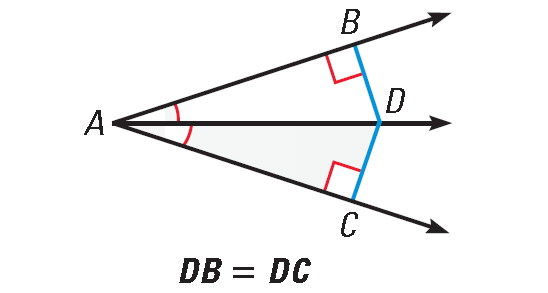
Proof of Angle Bisector Theorem :

Given :

D is on the bisector of ∠BAC, DB ⊥ AB, DC ⊥ AC.

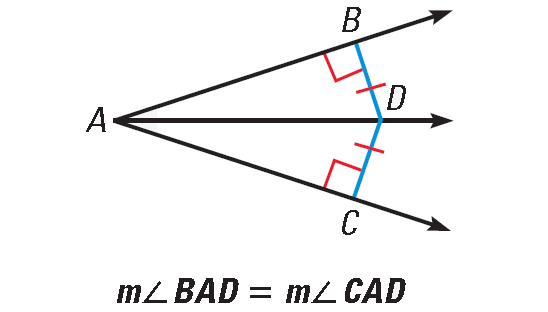
To Prove :

DB = DC

Plane for Proof :

Prove that ΔADB ≅ ΔADC.

Then conclude that DB ≅ DC, so DB = DC.

Proof :

By the definition of an angle bisector, ∠BAD ≅ ∠CAD.

Because ∠ABD and ∠ACD are right angles,

∠ABD ≅ ∠ACD

By the Reflexive Property of Congruence, AD ≅ AD.

By the AAS congruence theorem,

ΔADB ≅ ΔADC

Because corresponding parts of congruent triangles are congruent,

DB ≅ DC

By the definition of congruent segments,

DB = DC

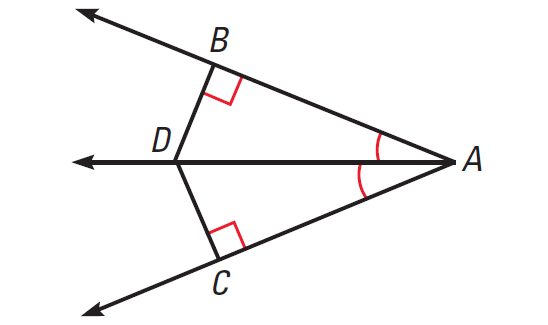
Converse of the Angle Bisector Theorem

If a point is in the interior of an angle and is equidistant from the sides of the angle, then it lies on the bisector of the angle.

If DB = DC, then

m∠BAD = m∠CAD

Solving Problems on Perpendiculars and Bisectors

Problem 1 :

In the diagram shown below, MN is the perpendicular bisector of ST.

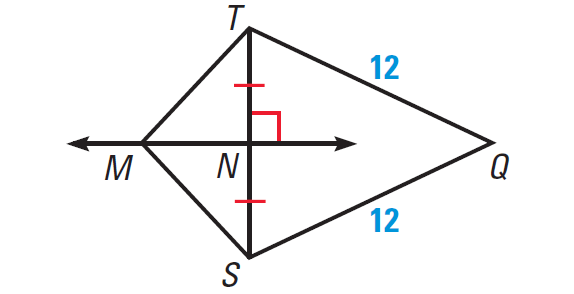
(a) What segment lengths in the diagram are equal?

(b) Explain why Q is on MN?

Answer (a) :

MN bisects ST, so NS = NT.

Because M is on the perpendicular bisector of ST, by Perpendicular Bisector Theorem,

MS = MT

The diagram shows that QS = QT = 12.

Answer (b) :

QS = QT, so Q is equidistant from S and T.

By Converse of the Perpendicular Bisector Theorem Q is on the perpendicular bisector of ST, which is MN.

Question 2 :

Some roofs are built with wooden trusses that are assembled in a factory and shipped to the building site. In the diagram of the roof truss shown below, we are given that AB bisects ∠CAD and that ∠ACB and ∠ADB are right angles. What can be said about BC and BD?

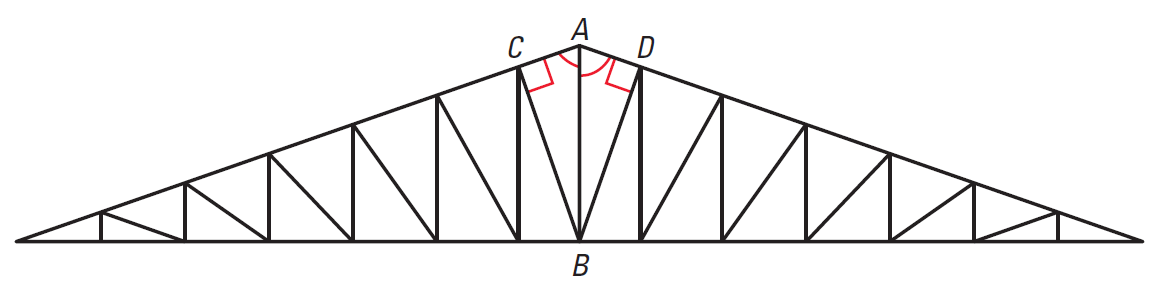
Answer :

Because BC and BD meet AC and AD at right angles, they are perpendicular segments to the sides of ∠CAD.

This implies that their lengths represent the distances from the point B to AC and AD.

Because point B is on the bisector of ∠CAD, it is equidistant from the sides of the angle.

So, BC = BD, and you can conclude that So,

BC ≅ BD

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.