PERMUTATION WORD PROBLEMS WITH SOLUTIONS

Problem 1 :

A student appears in an objective test which contain 5 multiple choice questions. Each question has four choices out of which one correct answer.

(i) What is the maximum number of different answers can the students give?

(ii) How will the answer change if each question may have more than one correct answers?

Solution :

(i) What is the maximum number of different answers can the students give?

Number of ways to answer the 1^st question  =  4

Number of ways to answer the 2^nd question  =  4

Number of ways to answer the 3^rd question  =  4

Number of ways to answer the 4^th question  =  4

Number of ways to answer the 5^th question  =  4

Number of ways  =  4 ⋅ 4⋅  4 ⋅ 4 ⋅ 4

  =  4⁵

So, the total number of ways is 4^5.

Problem 2 :

How many strings can be formed from the letters of the word ARTICLE, so that vowels occupy the even places?

Solution :

Letters in the word ARTICLE  =  {A, R, T, I, C, L, E}

Number of letters  =  7

Vowels  =  { A, I, E }  Others  =  { R, I, C, L }

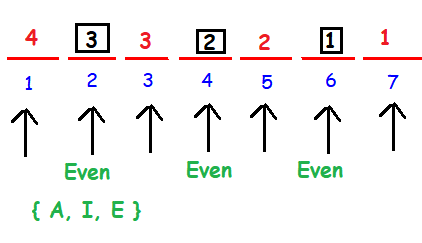
Even places are 2^nd, 4^th and 6^th.

In 2^nd place, we may fill any one of the letters {A, I, E}. So, we have 3 options to fill up the 2^nd place.

In 4^th place, we have 2 options. Because we have already used a letter in the second place.

In 6^th place, we have 1 option. Because we have already used two letters in the even places.

By applying the above rule in order to fill up the odd places, we get

1st place  =  4 options 

3rd place  =  3 options

5th place  =  2 options

7th place  =  1 option.

Number of ways  =  4 ⋅ 3 ⋅ 3 ⋅ 2 ⋅ 2 ⋅ 1 ⋅ 1

  =  144 ways

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.