PERMUTATION WITH REPETITION PROBLEMS WITH SOLUTIONS

Permutation With Repetition Problems With Solutions :

In this section, we will learn, how to solve problems on permutations using the problems with solutions given below.  

Permutation With Repetition Problems With Solutions - Practice questions

Question 1 :

8 women and 6 men are standing in a line.

(i) How many arrangements are possible if any individual can stand in any position?

(ii) In how many arrangements will all 6 men be standing next to one another?

(iii) In how many arrangements will no two men be standing next to one another?

Solution :

(i) How many arrangements are possible if any individual can stand in any position ?

Total number of members  =   14

The first person can choose any one of 14 places. So he or she has 14 options.

The 2nd person has 13 options. So each person will have 1 option less than the previous person has.

  =  14  ⋅ 13 ⋅ 12 ⋅ 11 ⋅ 10 ............. 1

So the total number of arrangements  =  14!

(ii) In how many arrangements will all 6 men be standing next to one another?

Solution :

Let us consider all 6 men as one unit. So, 8 women can choose their places out of 9 places (14 - 6). 

These 6 men can shuffle them in 6 places.

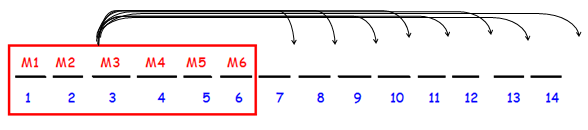
So, the number of arrangements for this case is 9! ⋅ 6!

(iii) In how many arrangements will no two men be standing next to one another?

Solution :

First, let us arrange the seats for women then, we may allot the seats for men between them.

Women are having 8 seating options. They may shuffle them into 8!.

Next considering the number of seating arrangements for men, we have 9 seats in between them. Out of these 9 seats, they may choose any 6.

So, the total number of ways  =  8! ⋅ ⁹P₆

Question 2 :

Find the distinct permutations of the letters of the word MISSISSIPPI?

Solution :

Since we have repeating letters, we have to use the concept given below.

Total number of letters  =  11

In the word "MISSISSIPPI", the letter "S" is appearing 4 times. "I" is appearing 4 times, "P" is appearing 2 times.

  =  11!/4!4!2!

  =  11 ⋅ 10 ⋅ 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4!/(4! 4! 2!)

  =  11 ⋅ 10 ⋅ 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 / (4 ⋅ 3 ⋅ 2 ⋅ 1)(2 ⋅ 1)

  =  34650

Hence the distinct permutations of the letters of the word is 34650.

After having gone through the stuff given above, we hope that the students would have understood, how to solve problems on permutations.

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.