PERMUTATION AND COMBINATION
PROBLEMS

Problem 1 :

Compute the sum of all 4 digit numbers which can be formed with the digits 1, 3, 5, 7, if each digit is used only once in each arrangement.  

Solution :

Number of numbers can be formed with the digits 1, 3, 5 and 7 is

4!  =  4 ⋅ 3 ⋅ 2 ⋅ 1

4!  =  24

Number of digits given  =  4 (they are 1,3,5 and 7) 

Number of times, each digit of (1, 3, 5, 7) will repeat in 1's place, 10's place, 100's place and 1000's place is 

=  (No. of numbers formed)/(No. of digits given) 

=  24/4

=  6

So, each of the given digits will occur six times in each of the place.

Sum of the digits in 1000's place is

=  (1 + 3 + 5 + 7) ⋅ 6

=  16 ⋅ 6

=  96

Similar is the case in 100's place, 10's place and 1's place.

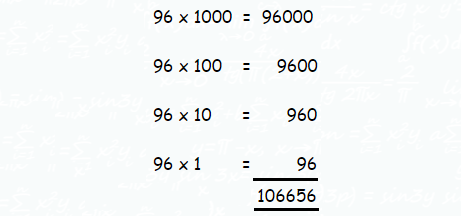
So, the sum of 4 digits numbers is 106656.

Problem 2 :

The number of 4 digit numbers greater than 5000 can be formed out of the digits 3, 4, 5, 6 and 7 (no digit is repeated). Find the number of such numbers. 

Solution : 

Given digits are 3, 4, 5, 6 and 7 and we form 4 digit numbers greater than 5000. 

1000's place ---> 3 choices (one out of  5,6,7)

100's place ---> 4 choices (Having 4 out of 5 digits) 

10's place ---> 3 choices (Having 3 out of 5 digits)

1's place ---> 2 choices (Having 2 out of 5 digits)

Number of numbers formed : 

=  3 ⋅ 4 ⋅ 3 ⋅ 2

=  72

Problem 3 :

An examination paper with 10 questions consists of 6 questions in Algebra and 4 questions in Geometry. At least one question from each section is to be attempted. In how many ways can this be done ?

Solution :

We have two alternatives for each question. That is, either we may attempt or we may not attempt. 

Therefore, no. of ways to attempt six questions in Algebra is 

=  2⁶

(But it includes the way of not attempting all the questions) 

So, no. of ways to attempt at least one question in Algebra is

=  2⁶ - 1

Similarly, number of ways to attempt at least one question in Geometry is

=  2⁴ - 1

Total number of ways for both the sections is

=  (2⁶ - 1) ⋅ (2⁴ - 1)

=  (64 - 1) ⋅ (16 - 1)

=  63 ⋅ 15

=  945

Problem 4 :

Find the total number of numbers greater than 2000 can be formed with the digits 1,2,3,4,5, no digit to be repeated in any number. 

Solution :

Given digits are 1,2,3,4, 5.It is not mentioned about how many digits can be used. So, we can form either 4 digit no. or 5 digit no. greater than 2000. 

Case 1 :

Forming 4 digit number greater than 2000

1000's place ---> 4 choices (one out of 2,3,4,5)

100's place ---> 4 choices (Having 4 out of 5 digits)

10's place ---> 3 choices (Having 3 out of 5 digits)

1's place ---> 2 choices (Having 2 out of 5 digits)

No. of numbers 4 digit numbers formed is

=  4 ⋅ 4 ⋅ 3 ⋅ 2

=  96

Case 2 :

Forming 5 digit number greater than 2000 

10000's place ---> 5 choices (1,2,3,4,5)

1000's place ---> 4 choices (Having 4 out of 5 digits)

100's place ---> 3 choices (Having 3 out of 5 digits)

10's place ---> 2 choices (Having 2 out of 5 digits)

1's place ---> 1 choice (Having 1 out of 5 digits)

No. of numbers 5 digit numbers formed is

=  5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1

=  120

Total no. of numbers greater than 2000 formed is

=  96 + 120

=  216

Problem 5 :

A family of four brothers and three sisters is to be arranged for a photograph in one row. In how many ways can they be seated if  no two sisters sit together ?

Solution :

Let us consider the following arrangement. 

__ B₁ __ B₂ __ B₃ __ B₄ __ 

(B_1, B_2, B_3, B₄ ---> Brothers)

If we make the sisters to be seated in any of the 3 out of 5 blanks in the above arrangement, no two sisters sit together. 

So, sisters can be seated in 5P3 ways.

Brothers can be seated in 4! 

Thus the total number of ways is

=  4! ⋅ 5P3

=  (4 ⋅ 3 ⋅ 2 ⋅ 1) ⋅ (5 ⋅ 4 ⋅ 3)

=  1440

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.