PERIMETERS AND AREAS OF SIMILAR FIGURES

For any polygon, the perimeter is the sum of the lengths of its sides and the area of the polygon is the number of square units contained in its interior. 

Perimeters of Two Similar Figures :

If two polygons are similar, then the ratio of their perimeters is the same as the ratio of the lengths of their corresponding sides.

For example, if two polygons are similar with the lengths of corresponding sides in the ratio of a : b, then the ratio of their perimeters is also a : b. 

Areas of Two Similar Figures : 

If two polygons are similar, then the ratio of their areas is not the same as the ratio of the lengths of their corresponding sides. 

Areas of Similar Polygons

Theorem :

If two polygons are similar with the lengths of corresponding sides in the ratio of a : b, then the ratio of their areas is 

a² : b²

It has been illustrated in the diagram shown below.

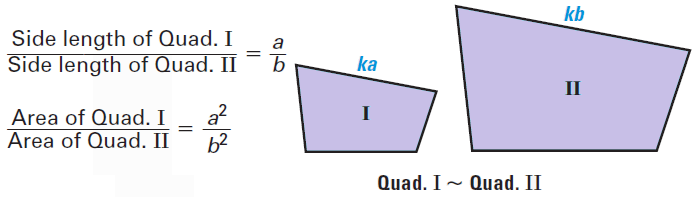
Finding Ratios of Similar Polygons

Example 1 : 

Pentagons ABCDE and LMNPQ shown below are similar. 

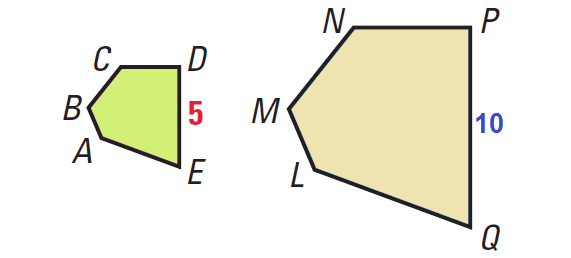
(a)  Find the ratio (red to blue) of the perimeters of the pentagons. 

(a) Find the ratio (red to blue) of the areas of the pentagons. 

Solution :

The ratio of the lengths of corresponding sides in the pentagons is 

=  5/10

=  1/2

=  1 : 2

Solution (a) : 

Because the ratio of the lengths of the corresponding sides is 1 : 2, the ratio of the perimeters is also 1 : 2. 

So, the perimeter of pentagon ABCDE is half the perimeter of pentagon LMNPQ. 

Solution (b) : 

The ratio of the lengths of the corresponding sides in the pentagons is 1 : 2. 

Using the Theorem, the ratio of the areas is 

=  1² : 2²

=  1 : 4

So, the area of pentagon ABCDE is one fourth the area of pentagon LMNPQ.

Finding Perimeters and Areas of Similar Polygons

Example 2 :

A trading pit at the Chicago Board of Trade is in the shape of a series of regular octagons. One octagon has a side length of about 14.25 feet and an area of about 980.4 square feet. Find the area of a smaller octagon that has a perimeter of about 76 feet.

Solution :

All regular octagons are similar because all corresponding angles are congruent and the corresponding side lengths are proportional.

Draw and label a sketch. 

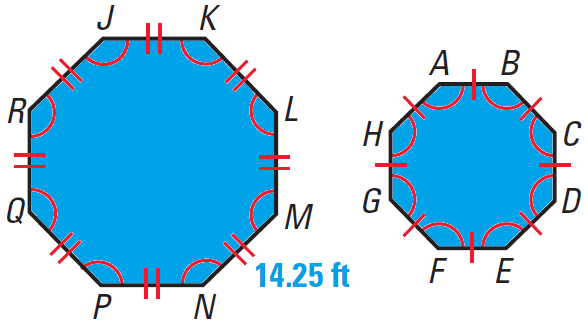
Find the ratio of the side lengths of the two octagons, which is the same as the ratio of their perimeters.

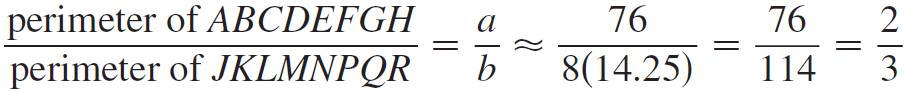
The ratio of the areas of the smaller octagon to the larger is 

=  a² : b²

=  2² : 3²

=  4 : 9

=  4/9

Calculate the area of the smaller octagon. Let A represent the area of the smaller octagon. 

Then, we have

A/980.4  =  4/9

Use cross product property. 

9A  =  4(980.4)

Simplify. 

9A  =  3921.6

Divide each side by 9. 

9A/9  =  3921.6/9

A  ≈  435.7

The area of the smaller octagon is about 435.7 square feet.

Using Areas of Similar Figures

Example 3 :

Mr. Alex is buying photographic paper to print a photo in different sizes. An 8 inch by 10 inch sheet of the paper costs $0.42. What is a reasonable cost for a 16 inch by 20 inch sheet ?

Solution :

The ratio of the lengths of the corresponding sides of the two rectangular pieces of paper is

=  8/16  or  10/20

=  1/2

=  1 : 2

The ratio of the areas of the pieces of paper is

=  1² : 2²

=  1 : 4

So, the area of larger piece of paper is four times the area of smaller piece of paper. 

Because the cost of the paper should be a function of its area, the larger piece of paper should cost about four times as much as the cost of smaller piece of paper.

Hence, the cost of larger piece of paper is 

=  4(0.42)

=  $1.68

Ratios of Similar Figures

Example 4 :

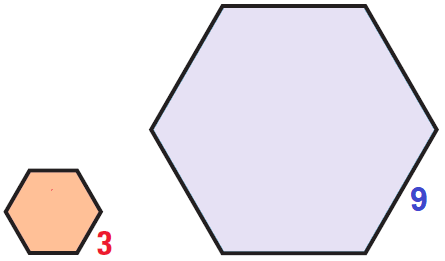
The red and blue figures shown below are similar. Find the ratio (red to blue) of their perimeters and of their areas. 

Solution :

Ratio of the perimeters :

The ratio of the lengths of corresponding sides in the hexagon is 

=  3/9

=  1/3

=  1 : 3

Hence, the ratio of the perimeters is also 1 : 3. 

Ratio of the areas :

The ratio of the lengths of the corresponding sides in the pentagons is 1 : 3. 

Using the Theorem, the ratio of the areas is 

=  1² : 3²

=  1 : 9

Example 5 : 

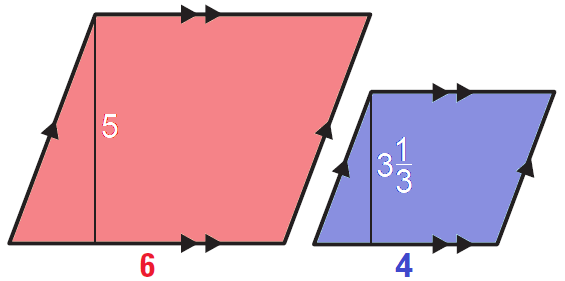
The red and blue figures shown below are similar. Find the ratio (red to blue) of their areas using the theorem and justify your answer. 

Solution :

The ratio of the lengths of corresponding sides in the parallelograms is 

=  6/4

=  3/2

=  3 : 2

The ratio of the lengths of the corresponding sides in the  parallelograms is 3 : 2. 

Using the Theorem, the ratio of the areas is 

=  3² : 2²

=  9 : 4

Justification : 

Area of red parallelogram is 

=  base ⋅ height

=  6 ⋅ 5

=  30 square units

Area of blue parallelogram is 

=  base ⋅ height

=  4 ⋅ 3⅓

=  4 ⋅ 10/3

=  40/3 square units. 

Ratio of the areas of parallelograms is 

=  30 : 40/3

=  90 : 40

=  9 : 4

Hence, the ratio of the areas found  9 : 4 using Theorem is reasonable. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.