PERIMETER OF RHOMBUS WORKSHEET

1. Find the perimeter of the rhombus whose side length is 16 cm.

2. If the perimeter of a rhombus is 72 inches, then find the length of each side.

3. A rhombus has side length of 500 cm. Find its perimeter in meter.

4. If the length of each side of a rhombus is (3x + 4) and its perimeter is 76 units, find the value of x.

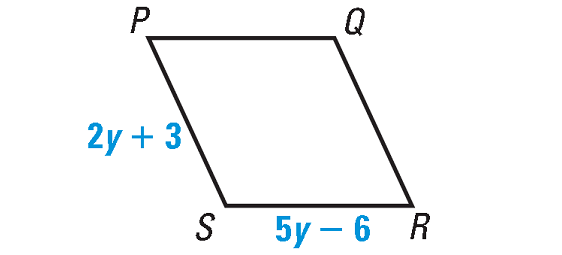
5. In the diagram shown below, if PQRS is a rhombus, then find its perimeter.

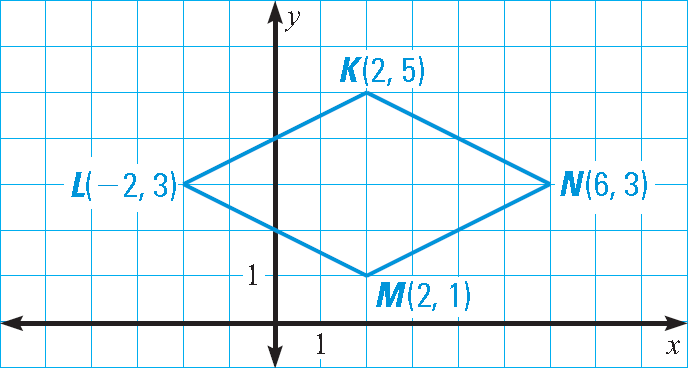
6. Find the perimeter of the rhombus shown below.

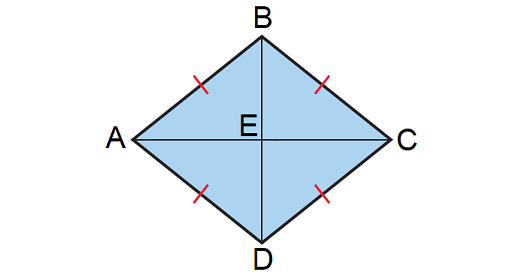
7. In the rhombus ABCD shown below, if the lengths of the diagonals AC and BD are 10 units and 8 units respectively, find its perimeter.

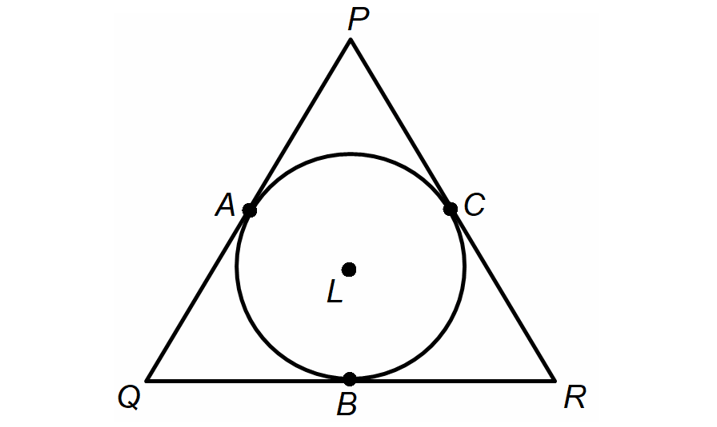
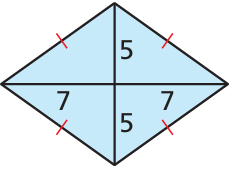
8.  find the area and perimeter of the kite or rhombus.

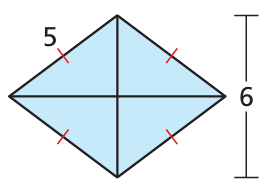
9. find the area and perimeter ofrhombus.

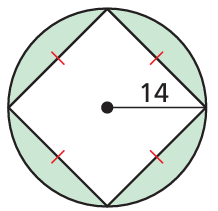
10. find the area of the shaded region.

11. One diagonal of a rhombus is four times the length of the other diagonal. The area of the rhombus is 98 square feet. Find the length of each diagonal.

1. Answer :

Formula for perimeter of a rhombus :

=  4s 

Substitute 16 for s.

=  4(16)

=  64

So, the perimeter of the rhombus is 64 cm.

2. Answer :

Perimeter of the rhombus  =  72 inches

4s  =  72

Divide each side by 4.

 s  =  16 

So, the length of each side of the rhombus is 16 inches. 

3. Answer :

Formula for perimeter of a rhombus :

=  4s 

Substitute 500 for s.

=  4(500)

=  2000 cm -----(1)

We know  

100 cm  =  1 m

Therefore, to convert centimeter to meter,  we have to divide by 100. 

(1)-----> Perimeter  =  2000 cm

Divide the right side by 100 to convert cm into m.

Perimeter  =  (2000 / 100) m

=  20 m

So, perimeter of the rhombus is 20 meters.

4. Answer :

Perimeter of the rhombus  =  76 units

4s  =  76

Divide each side by 4.

s  =  19

Substitute (3x + 4) for s. 

3x + 4  =  19

Subtract 4 from each side. 

3x  =  15

Divide each side by 3. 

x  =  5

5. Answer :

All four sides of a rhombus are congruent. 

So, 

RS  =  PS

5y - 6  =  2y + 3

Subtract 2y from each side.

3y - 6  =  3

Add 6 to each side. 

3y  =  9

Divide each side by 3. 

y  =  3

To find the length of each side of the rhombus, substitute 3 for y either in '2y + 3' or '5y - 6'.

2y + 6  =  2(3) + 3

2y + 6  =  6 + 3

2y + 6  =  9

So, the length of each side of the rhombus is 9 units. 

Formula for perimeter of a rhombus :

=  4s 

Substitute 9 for s.

=  4(9)

=  36

So, perimeter of the rhombus is 36 units. 

6. Answer :

Find the length of the side MN in the above rhombus using distance formula. 

MN  =  √[(x₂ - x₁)² + (y₂ - y₁)²]

Substitute (x₁, y₁)  =  (2, 1) and (x₂, y₂)  =  (6, 3).  

LM  =  √[(x₂ - x₁)² + (y₂ - y₁)²]

LM  =  √[(6 - 2)² + (3 - 1)²]

LM  =  √(4² + 2²)

LM  =  √(16 + 4)

LM  =  √20

LM  =  2√5

All four sides of a rhombus are congruent. 

Then, the length of each side of the above rhombus is 2√5 units. 

Formula for perimeter of a rhombus :

=  4s 

Substitute 2√5 for s.

=  4(2√5)

=  8√5

So, perimeter of the rhombus is 8√5 units. 

7. Answer :

The diagonals of a rhombus will be perpendicular and they will bisect each other. 

Then, we have

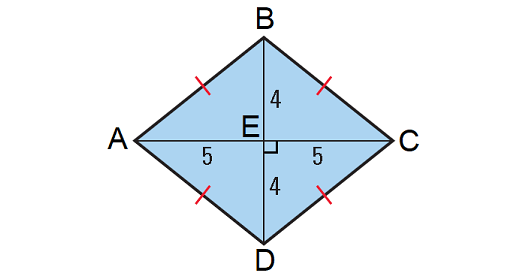
In the above rhombus, consider the right angled triangle CDE. 

By Pythagorean Theorem, 

CD²  =  DE² + CE²

CD²  =  4² + 5²

CD²  =  16 + 25

CD²  =  41

CD  =  √41

All four sides of a rhombus are congruent. 

Then, the length of each side of the above rhombus is √41 units. 

Formula for perimeter of a rhombus :

=  4s 

Substitute √41 for s.

=  4√41

So, perimeter of the rhombus is √41 units. 

8. Answer :

Let x be the side length of rhombus.

Using Pythagorean theorem,

x² = 5² + 7²

x² = 25 + 49

x² = 74

x = √74

Area of rhombus = (1/2) x d₁ x d₂

= (1/2) x (5 + 5) x (7 + 7)

= (1/2) x 10 x 14

= 5 x 14

= 70 square units.

Perimeter of rhombus = 4(side length)

= 4√74 units

9. Answer :

Length of one diagonal = 6, half length = 3

Let x be the half length of another diagonal.

x² + 3² = 5²

x² = 25 - 9

x² = 16

x = 4

Length of another diagonal is 2(4) = 8

Area of rhombus = (1/2) x 6 x 8

= 3 x 8

= 24 square units

Perimeter of rhombus = 4(side)

= 4(5)

= 20 units.

10. Answer :

We have rhombus which is inside the circle.

Radius of circle = 14 units

half length of diangonals = 14 units and let x be the side length of rhombus.

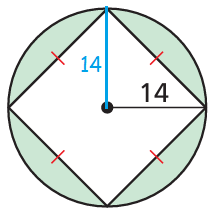
14² + 14² = x²

x² = 196 + 196

x² = 392

x = √392

x = √2 x (196)

x = 14 √2

Area = (1/2) x  28 x 28

= 392 square units.

Area of circle = πr²

= 3.14(14)²

= 3.14 (196)

= 615.44 square units

Shadded region = 615.44 - 392

= 223.44 square units,

11. Answer :

Let d₁ and d₂ be the lengths of diagonal.

d₁ = 4d₂

Area of rhombus = 98 square units

(1/2) x 4d₂ x d₂ = 98

2(d₂)² = 98

(d₂)² = 49

d₂ = 7

d₁ = 4(7)

= 28

So, the length of diagonals are 28 feet and 7 feet.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.