PERIMETER OF RECTANGLE WORKSHEET

Problem 1 :

The length and width of a rectangle are 16 cm and 12 cm respectively. Find its perimeter. 

Problem 2 :

If the perimeter of a rectangle is 50 cm and its length is 15 cm, then find its width. 

Problem 3 :

The area of the rectangle is 150 square inches. If the length is twice the width, then find its perimeter. 

Problem 4 :

The length of a rectangle is 3 ft and one of the diagonal measures √13 ft. Find its perimeter. 

Problem 5 :

The length of a rectangle is 3 yards more than its width and its perimeter is 18 yards. Find its length and width.

Problem 6 :

The length and width of a rectangle are in the ratio 3 : 4 and its perimeter is 98 inches. Find its length and width. 

Problem 7 :

Mr. John would like to fence his rectangular shaped garden. The length of the garden is 13 ft and width is 10 ft. If the cost of fencing is $8 per feet, then find the total cost of fencing for the entire garden. 

Problem 8 :

The length of  a rectangle is 70 cm and width is 30 cm. If the length is increased by 10% and width is by 20%, then find the percentage increase in perimeter. 

Solutions

Problem 1 :

The length and width of a rectangle are 16 cm and 12 cm respectively. Find its perimeter. 

Solution:

Formula for perimeter of a rectangle :

=  2(l + w) 

Substitute 16 for l and 12 for w.

=  2(16 + 12)

=  2(28)

=  56

So, the perimeter of the rectangle is 56 cm.

Problem 2 :

If the perimeter of a rectangle is 50 cm and its length is 15 cm, then find its width. 

Solution:

Perimeter of the rectangle  =  50 cm

2(l + w)  =  50

Divide each side by 2.

 l + w  =  25

Substitute 15 for l.

15 + w  =  25

Subtract 15 from each side.

w  =  10

So, the width of the rectangle is 10 cm. 

Problem 3 :

The area of the rectangle is 150 square inches. If the length is twice the width, then find its perimeter. 

Solution:

Let x be the width of the rectangle. 

Then, the length of the rectangle is 2x.

Area of the rectangle  =  150 in²

l ⋅ w  =  150

x ⋅ 2x  =  150

2x²  =  150

Divide each side by 2.

x²  =  75

Find positive square root on both sides.

√x²  =  √75

x  =  √(5 ⋅ 5 ⋅ 3)

x  =  5√3

Therefore, the width of the rectangle is 5√3 in.

Then, the length of the rectangle is 

=  2 ⋅ width

=  2 ⋅ 5√3

=  10√3 in

Formula for perimeter of a rectangle :

=  2(l + w)

Substitute 10√3 for l and 5√3 for w. 

=  2(10√3 + 5√3)

=  2(15√3)

=  30√3

So, the perimeter of the rectangle is 30√3 in. 

Problem 4 :

The length of a rectangle is 3 ft and one of the diagonal measures √13 ft. Find its perimeter. 

Solution:

To find the perimeter of a rectangle, we have to know its length and width. Length is given in the question, that is 3 ft. So, find its width. 

Draw a sketch. 

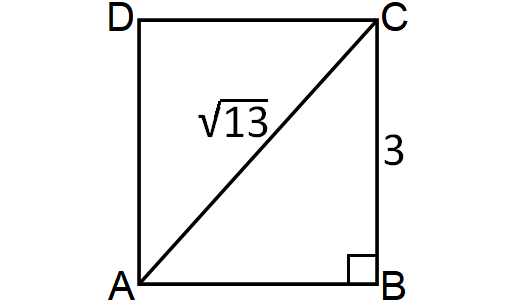
In the figure shown above, consider the right triangle ABC. 

By Pythagorean Theorem, we have

AB² + BC²  =  AC²

Substitute.

AB² + 3²  =  (√13)²

Simplify and solve for AB. 

AB² + 9  =  13

Subtract 9 from each side. 

AB²  =  4

Find positive square root on both sides.

 √AB²  =  √4

AB  =  2

Therefore, the width of the rectangle is 2 ft. 

Formula for perimeter of a rectangle.

=  2(l + w)

Substitute 3 for l and 2 for w.

=  2(3 + 2)

=  2(5)

=  10

So, the perimeter of the rectangle is 10 ft. 

Problem 5 :

The length of a rectangle is 3 yards more than its width and its perimeter is 18 yards. Find its length and width.

Solution:

Let x be the width of the rectangle.

Then, the length of the rectangle is (x + 3) yards. 

Perimeter of the rectangle  =  18 yards

2(l + w)  =  18

Divide each side by 2. 

l + w  =  9

Substitute (x + 3) for l and x for w. 

(x + 3) + x  =  9

x + 3 + x  =  9

2x + 3  =  9

Subtract 3 from each side. 

2x  =  6 

Divide each side by 2. 

x  =  3

x + 3  =  6

So, the length and width of the rectangle are 6 yards and 3 yards respectively.

Problem 6 :

The length and width of a rectangle are in the ratio 3 : 4 and its perimeter is 98 inches. Find its length and width. 

Solution:

From the ratio 3 : 4, let the length and width of the rectangle be 3x and 4x respectively.

Perimeter of the rectangle  =  98 inches

2(l + w)  =  98

Divide each side by 2.

l + w  =  49

Substitute 3x for l and 4x for w.

3x + 4x  =  49

7x  =  49

Divide each side by 7.

x  =  7

Length  =  3x  =  3(7)  =  21 in

Width  =  4x  =  4(7)  =  28 in

So, the length and width of the rectangle are 21 inches and 28 inches respectively. 

Problem 7 :

Mr. John would like to fence his rectangular shaped garden. The length of the garden is 13 ft and width is 10 ft. If the cost of fencing is $8 per feet, then find the total cost of fencing for the entire garden. 

Solution:

To find the total cost of fencing the entire garden, we have to know the perimeter of the garden. So, find the perimeter. 

Formula for perimeter of a rectangle :

=  2(l + w)

Substitute 13 for l and 10 for w. 

=  2(13 + 10)

=  2(23)

=  46 ft

Therefore, the perimeter of the garden is 46 ft.

The cost of fencing is $8 per feet.

Then, the total cost of fencing 46 ft :

=  46 ⋅ 8

=  368

So, the total cost of fencing for the entire garden is $368.

Problem 8 :

The length of  a rectangle is 70 cm and width is 30 cm. If the length is increased by 10% and width is by 20%, then find the percentage increase in perimeter. 

Solution:

Before increase in length and width :

Formula for perimeter of a rectangle :

=  2(l + w)

Substitute 70 for l and 30 for w. 

=  2(70 + 30)

=  2(100)

=  200 cm

Therefore, the perimeter of the rectangle is 200 cm.

After increase in length and width :

Length  =  (100 + 10)% of 70  =  1.1 ⋅ 70  =  77 cm

Width  =  (100 + 20)% of 30  =  1.2 ⋅ 30  =  36 cm

Formula for perimeter of a rectangle :

=  2(l + w)

Substitute 77 for l and 36 for w. 

=  2(77 + 36)

=  2(113)

=  226 cm

Therefore, the perimeter of the rectangle is 226 cm.

Percentage increase in perimeter :

Increase in perimeter  =  226 - 200

Increase in perimeter  =  26 cm

Percentage increase in perimeter  =  (26 / 200) ⋅ 100 %

Percentage increase in perimeter  =  13%

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.