PERIMETER OF PARALLELOGRAM WORKSHEET

1. Find the perimeter of a parallelogram with the base and side length are 15 cm and 12 cm.

2. Find the perimeter of parallelogram with the base and side length are 9 ft and 3 ft.

3. If the perimeter of parallelogram is 40 in and its base is 15 in, find its side length.

4. Prove that the points (5, 8), (6, 3), (3, 1) and (2, 6) form a parallelogram and also find the perimeter.

5. Ana knows that the perimeter of her backyard is (6x² + 14x) feet. If the length of her backyard is (2x² + 3x – 7) feet, what is the width of her backyard?

6. The length of the rectangular garden is 4 less than twice the width. Find the perimeter and area of the garden.

7. If the area of parallelogram with lenght 4x is 4x² + 12x, find the height.

8. You are decorating the bulletin board in your classroom with pictures of your classmates. Each picture covers an area of 4x cm². The area of the board is 4x² + 16x cm². Write an expression to represent how many pictures are required to cover the board.

9.  The length of a cement pad on a playground is 3 m longer than the width. The width is 5x m.

a) Write an expression for the area of the cement pad.

b) If x = 2 m, what is the area of the cement pad?

10.  Altitudes MN and MO of parallelogram MGHK are 8 cm and 4 cm long respectively. One side GH is 6 cm long. Find the perimeter of MGHK.

1. Answer :

Perimeter of a parallelogram :

= 2(a + b)

Substitute a = 15 and b = 12.

= 2(15 + 12)

= 2(27)

= 54 cm

2. Answer :

Perimeter of a parallelogram :

= 2(a + b)

Substitute a = 9 and b = 3.

= 2(9 + 3)

= 2(12)

= 24 cm

3. Answer :

Perimeter of a parallelogram = 40

2(a + b) = 40

Substitute a = 15.

2(15 + b) = 40

30 + 2b = 40

Subtract 30 from each side.

2b = 10

Divide each side by 2.

b = 5

The side length of the parallelogram is 5 in.

4. Answer :

Let A(5, 8), B(6, 3), C(3, 1) and D(2, 6).

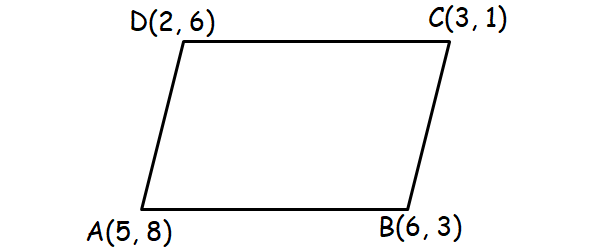
Formula to find the distance between two points :

d = √[(x₂ - x₁)² + (x₂ - x₁)²]

Length of AB :

Substitute (x₁, y₁) = A(5, 8) and (x₂, y₂) = B(6, 3) in the distance formula.

AB = √[(6 - 5)² + (3 - 8)²]

= √[(1)² + (-5)²]

= √[1 + 25]

= √26

Length of BC :

Substitute (x₁, y₁) = B(6, 3) and (x₂, y₂) = C(3, 1) in the distance formula.

BC = √[(3 - 6)² + (1 - 3)²]

= √[(-3)² + (-2)²]

= √[9 + 4]

= = √13

Length of DC :

Substitute (x₁, y₁) = D(2, 6) and (x₂, y₂) = C(3, 1) in the distance formula.

DC = √[(3 - 2)² + (1 - 6)²]

= √[(1)² + (-5)²]

= √[1 + 25]

= = √26

Length of AD :

Substitute (x₁, y₁) = A(5, 8) and (x₂, y₂) = D(2, 6) in the distance formula.

AD = √[(2 - 5)² + (6 - 8)²]

= √[(-3)² + (-2)²]

= √[9 + 4]

= = √13

length of AB = length of DC

length of AD = length of BC

Opposite sides are equal. So, the given points form a parallelogram.

Perimeter = 2(√26 + √13) units

5. Answer :

Perimeter of backyard = 6x² + 14x

Length = 2x² + 3x – 7

Width = ?

2(length + width) = 6x² + 14x

2(2x² + 3x – 7 + Width) = 6x² + 14x

(2x² + 3x – 7 + Width) = (6x² + 14x)/2

(2x² + 3x – 7 + Width) = 3x² + 7x

Width = 3x² + 7x - 2x² - 3x + 7

Width = x² + 4x + 7

So, the width of the rectangle is x² + 4x + 7.

6. Answer :

Let x be the width of the rectangle.

Length = 2x - 4

Perimeter of the rectangular garden = 2(length + width)

= 2(2x - 4 + x)

= 2(3x - 4)

Perimeter of the rectangle = 2(3x - 4)

Area of rectangle = length x width

= (2x - 4) x

= 2x² - 4x

7. Answer :

In parallelogram, length = 4x

Area = 4x² + 12x

Height be the unknown.

Area of parallelogram = base (height)

4x² + 12x = 4x (height)

Height = (4x² + 12x) / 4x

= x + 3

So, the height of the parallelogram is x + 3.

8. Answer :

The area of the board = 4x² + 16x cm²

Area covered by one picture = 4x cm²

Number of pictures to be covered = (4x² + 16x)/4x

= x + 4

Required number of pictures is being represented with the expression x + 4.

9. Answer :

Width = 5x

Length = 5x + 3

a) Area of cement pad = length x width

= (5x + 3) 5x

b) When x = 2 m

= (5(2) + 3)5(2)

= 10 (10 + 3)

= 10(13)

= 130 m²

10. Answer :

In triangle MKO,

MK² = MO² + OK²

MN = 8 cm and MO = 4 cm

GH = MK (opposite sides)

6² = OK² + 4²

OK² =  6² - 4²

= 36 - 16

OK² = 20

OK = √20

= √(2 x 2 x 5)

OK = 2√5

Area of parallelogram = base x height

= GH x MN

= 6 x 8

= 48

When MO = height, then base = HK

4 x HK = 48

HK = 48/4

= 12

Perimeter of parallelogram = 2(GH + HK)

= 2(6 + 12)

= 2(18)

= 36 cm

So, the perimeter of the parallelogram is 36 cm.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.