PERIMETER AND AREA OF RECTANGLE WORKSHEET

Problem 1 :

Find the perimeter of the figure shown below.

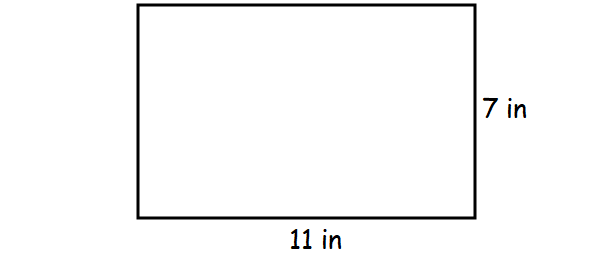
Problem 2 :

The perimeter of a rectangle is 42 cm. If its width is 3 more than twice its length, then find its length and with. 

Problem 3 :

The length of  a rectangle is 10 inches and its perimeter 36 inches. If the length is increased by 5 inches and width is increased by x inches, the perimeter is increased by 14 inches. Find the value of x. 

Problem 4 :

Find the area of the figure shown below.

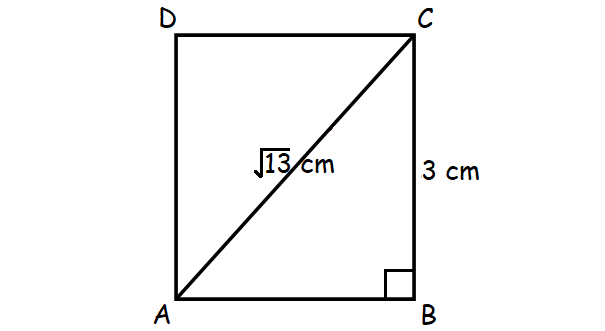
Problem 5 :

The length and width of a rectangular shaped wall are 8 ft and 12 ft respectively. If the cost of painting is $8.50 per square feet, then find the total cost of painting for the wall.  

Problem 6 :

The length of  a rectangle is 70 cm and width is 50 cm. If both the length and width of the rectangle are increased by 10%, find the percentage increase in area. 

Problem 7 :

If the area of a rectangular field is 2000 square meters and its perimeter is 180 meters, then find the length and width of the rectangle. 

Problem 8 : 

The poster has a border whose width is 2 cm on each side. If the printed material has the length of 6 cm and width of 8 cm, then find the area of the border.  

Answers

1. Answer :

The figure shown above is a rectangle with 7 inches length and 11 inches width. 

Formula for perimeter of a rectangle :

=  2(l + w) 

Substitute 7 for l and 11 for w.

=  2(7 + 11)

=  2(18)

=  36

So, the perimeter of the rectangle is 36 inches.

2. Answer :

Let x be the length of the rectangle. 

Then, the width is (2x + 3)

Perimeter of the rectangle  =  42 cm

2(l + w)  =  42

Divide each side by 2.

 l + w  =  21

Substitute x for l and (2x + 3) for w.

x + (2x + 3)  =  21

x + 2x + 3  =  21

3x + 3  =  21

Subtract 3 from each side.

3x  =  18

Divide each side by 3.

x  =  6

Therefore, the length is 6 cm.

And the width is

2x + 3  =  2(6) + 3

2x + 3  =  12 + 3

2x + 3  =  15

So, the length and width of the rectangle are 6 cm and 15 cm respectively.  

3. Answer :

Let w be the original width of the rectangle. 

Before increase in length and width :

Perimeter of the rectangle  =  36 in

2(l + w)  =  36

Divide each side by 2. 

l + w  =  18

Substitute 10 for l.  

10 + w  =  18

Subtract 18 from each side. 

w  =  8

After increase in length and width :

Length  =  10 + 5  =  15 in

Width  =  (8 + x) in

Perimeter of the rectangle  =  50 in

2(l + w)  =  50

Divide each side by 2.

l + w  =  25

Substitute 15 for l and (8 + x) for w. 

15 + (8 + x)  =  25

15 + 8 + x  =  25

23 + x  =  25

Subtract 23 from each side.

x  =  2

So, the value of x is 2. 

4. Answer :

The figure shown above is a rectangle with 3 cm length and the measure of one the diagonals is √13 cm. 

To find the area of a rectangle, we have to know its length and width. In the figure shown above, length is given, that is 3 cm. So, find its width. 

In the figure shown above, consider the right triangle ABC. 

By Pythagorean Theorem, we have

AB² + BC²  =  AC²

Substitute.

AB² + 3²  =  (√13)²

Simplify and solve for AB. 

AB² + 9  =  13

Subtract 9 from each side. 

AB²  =  4

Find positive square root on both sides.

 √AB²  =  √4

AB  =  2

Therefore, the width of the rectangle is 2 cm. 

Formula for area of a rectangle :

=  l ⋅ w

Substitute 3 for l and 2 for w.

=  3 ⋅ 2

=  6

So, the perimeter of the rectangle is 6 square cm.  

5. Answer :

To find the total cost of painting for the wall, we have to know its area. Because the wall is rectangle shaped, we can use the formula for area of a rectangle to find the area of the wall.    

Formula for area of a rectangle :

=  l ⋅ w

Substitute 8 for l and 12 for w.

=  8 ⋅ 12

=  96

So, the area of the wall is 96 square ft.

The cost of painting is $8.50 per square ft. 

Then, the total cost of painting for 96 square ft : 

=  96 ⋅ 8.50

=  816

So, the total cost of painting the wall is $816.

6. Answer :

Before increase in length and width :

Formula for area of a rectangle :

=  l ⋅ w

Substitute 70 for l and 50 for w. 

=  70 ⋅ 50

=  3500

Therefore, the area of the rectangle is 3500 square cm.

After increase in length and width :

Length  =  (100 + 10)% of 70  =  1.1 ⋅ 70  =  77 cm

Width  =  (100 + 10)% of 50  =  1.2 ⋅ 50  =  55 cm

Formula for area of a rectangle :

=  l ⋅ w

Substitute 77 for l and 55 for w. 

=  77 ⋅ 55

=  4235 

Therefore, the area of the rectangle is 4235 square cm.

Percentage increase in area :

Increase in area  =  4235 - 3500

Increase in area  =  735 cm²

Percentage increase in area  =  (735 / 3500) ⋅ 100 %

Percentage increase in area  =  21%

7. Answer :

Let x and y be the length and width of the rectangle respectively.

Perimeter of the rectangle  =  180 m

2(x + y)  =  180

Divide each side by 2.

x + y  =  90

Subtract x from each side.

y  =  90 - x -----(1)

Area of the rectangle  =  2000 m²

x ⋅ y  =  2000

Substitute (90 - x) for y.

x ⋅ (90 - x)  =  2000

90x - x²  =  2000

- x² + 90x  =  2000

Subtract 2000 from each side.

-x² + 90x - 2000  =  0

Multiply each side by negative sign. 

x² - 90x + 2000  =  0

Factor.

(x - 40)(x - 50)  =  0

x - 40  =  0     or     x - 50  =  0

x  =  40     or     x  =  50

The length is 40 meters or 50 meters.

If the length is 40 meters, then the width is

(1)-----> y  =  90 - 40

y  =  50 m

If the length is 50 meters, then the width is

(1)-----> y  =  90 - 50

y  =  40 m

So, the length and width are (40 m, 50 m) or (50 m , 40 m)

8. Answer :

Draw a sketch

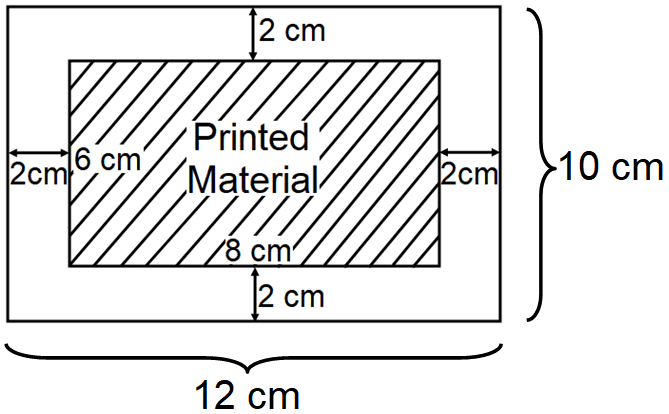
In the above diagram, to find the area of the border, we have to subtract the area of the printed material from the complete area of the poster. 

Complete area of the poster : 

=  l ⋅ w

Substitute 10 for l and 12 for w. 

=  10 ⋅ 12

=  120 cm² 

Area of the poster is 120 square cm.

Area of the printed material : 

=  l ⋅ w

Substitute 6 for l and 8 for w. 

=  6 ⋅ 8

=  48 cm² 

Area of the printed material is 48 square cm.

Area of the border :

=  Area of the poster - Area of the printed material

=  120 - 48

=  72 cm²

So, the area of the border is 72 square cm. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.