PERCENTAGE OF A NUMBER

Let us consider '30 percent of 500'.

30 percent means the value 30 is considered for one hundred. 

If 30 is the value considered for 100, what value can be considered for 500 ?

It can be calculated as follows.

30 % x 500  =  0.3 x 500  =  150

The picture given below clearly illustrates "How to find percentage of a number"

Here, the "Wh" question "what" has always to be replaced by some variable, say m.  

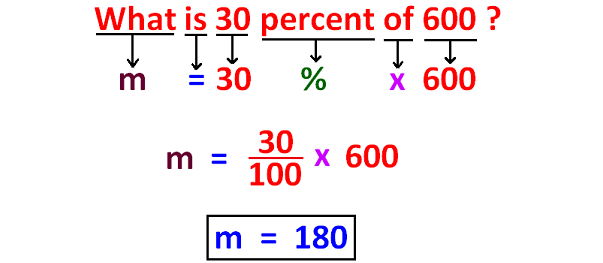
Sometimes, we will have the above question in a different method. It has been illustrated in the picture given below.

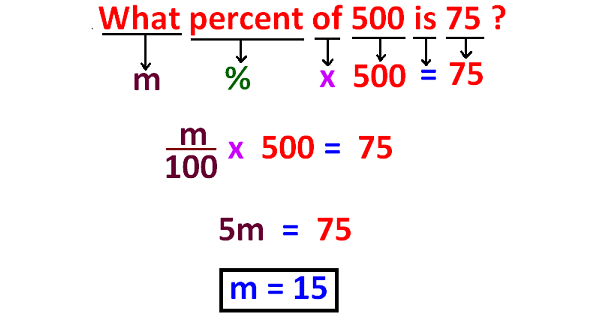
Practice Problems

Problem 1 :

What is 20% of 50 ?

Solution :

Let us replace "what" by some variable, say "m"

m  =  20%  50

m  =  0.2 ⋅ 50  

m  =  10

So, 20% of 50 is 10.

Problem 2 :

If 20% of 30 is equal to m% of 60, find the value of "m". 

Solution :

From the given information, we can have 

20% of 30  =  m% of 60

0.2 ⋅ 30  =  (m/100) ⋅ 60

6  =  3m / 5

5/3 ⋅ 6  =  m

10  =  m    

So, the value of "m" is 10.

Problem 3 :

If m percent of 500 is 75, what is m% of 700 ? 

Solution :

Our first aim is to get the value of "m" 

Given : "m" percent of 500 is 75

(m/100) ⋅ 500  =  75

5m  =  75

m  =  15

Target : m% of 700

m% of 700  =  15 % of 700

=  0.15 ⋅ 700

=  105

So, m% of 700 is 105.

Problem 4 :

David gets 20% income on $5000 investment per year. At the same rate, what is his income in 3 years ?

Solution :

Income for one year : 

20% of 5000  =  0.2 ⋅ 5000  =  1000

Income for 3  years :

=  3 ⋅ 1000

=  3000

So, David's income for 3 years is $3000.

Problem 5 :

John gets 15% income on $2500 investment per year. At the same rate, what is his income for 2.5 years ?

Solution :

Income for one year : 

15% of 2500  =  0.15 ⋅ 2500  =  375

Income of 2.5 years :

=  2.5 ⋅ 375

=  937.50

So, John's income for 2.5 years is $937.50

Problem 6 :

A gets 30% income on $7500 investment per year. If B gets the same income on $12500 investment per year, what is the percentage of income of "B" ? 

Solution :

Let "m" be the  percentage of income of B 

From the given information, we have 

30% of 7500  =  m% of 12500

0.3 ⋅ 7500  =  (m/100) ⋅ 12500

2250  =  125m

2250/125  =  m

18  =  m 

So, the percentage of income of B is 18%. 

Problem 7 :

A trader gets 25% profit on all the products. If the cost price of a particular product is $350, find his profit.  

Solution :

Given : 25% profit on all the products

So, profit on $350  =  25% ⋅ 350

=  0.25 ⋅ 350

=  87.5

So, the required profit is $87.50

Problem 8 :

A trader gets $6.25 profit on a product whose cost price is $125. 

What is profit percentage ?

Solution :

Let "m" be the required percentage. 

From the given information, we can have 

m% of 125  =  6.25

(m/100) ⋅ 125  =  6.25

m  =  (6.25/125) ⋅ 100

m  =  5    

So, the profit percentage is 5%.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.