PERCENTAGE INCREASE AND DECREASE WORD PROBLEMS

Formula to find percentage increase/decrease

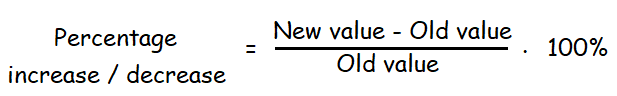
Problem 1 :

The price of a TV is $260. In a sale the price is decreased by 20%. Work out the price of the TV sale.

Solution :

Price of the TV = $260

It is given that the price of the TV is decreased by 20%.

Then, the selling price of the TV :

= 80% of 260

= 0.80(260)

= $208

Problem 2 :

The value of a painting rises from $120000 to $192000. Work out the percentage increase in the value of painting.

Solution :

Original price of the painting = $120000

After increase, the new price = $192000.

Price increase = 192000 - 120000

= $72000

Percentage increase :

= ⁷²⁰⁰⁰⁄₁₂₀₀₀₀ ⋅ 100%

= ⅗ ⋅ 100%

= 3 ⋅ 20%

= 60%

The value of the paiting is increased by 60%.

Problem 3 :

A puppy weighed 2 kg. Eight weeks later the puppy weighed 3.5 kg. What was the percentage increase in the Puppy's weight?

Solution :

Weight of puppy = 2 kg.

Puppy's weight after eight weeks = 3.5 kg.

Increase in weight in eight weeks :

= 3.5 - 2

= 1.5 kg.

Percentage increase :

= (1.5/2) ⋅ 100% 

= 0.75 ⋅ 100%

= 75%

Puppy's weight was increased by 75%.

Problem 4 :

Peter's weight decreases from 80 kg. to 64 kg. Calculate the percentage decrease in Peter's weight.

Solution :

Old weight = 80 kg.

New weight = 64 kg.

Decrease in weight :

= 80 - 64

= 16 kg.

Percentage decrease :

= ¹⁶⁄₈₀ ⋅ 100%

= ⅕ ⋅ 100%

= 1 ⋅ 20%

= 20%

Peter has reduced 20% of his weight.

Problem 5 :

Alice buys a book for $19.80 A year later she sells the book for $12.87 Calculate the percentage decrease in the value of the book.

Solution :

Cost price of the book = $19.80

Selling price = $12.87

Decrease in the price :

= 19.80 - 12.87

= $6.93

Percentage decrease :

= (6.93/19.80) ⋅ 100%

= 35%

The value of the book is decaresed by 35%.

Problem 6 :

The volume of juice in a can is increased from 250 ml. to 330 ml. Work out the percentage increase.

Solution :

Original volume of juice in a can = 250 ml.

Volume of juice in can after increase = 330 ml.

Increase in volume :

= 330 - 250

= 80 ml.

Percentage increase :

= ⁸⁰⁄₂₅₀ ⋅ 100%

= ⁸⁄₂₅ ⋅ 100%

= 8 ⋅ 4%

= 32%

Volume of juice in can is increased by 32%.

Problem 7 :

Sarah bought a TV for $250. Three years later she sold it for $180. Work out her percentage loss.

Solution :

Cost price of the TV = $250

Selling price = $180

Cost price > Selling price ----> Loss

Loss = Cost price - Selling price

= 250 - 180

= $70

Percentage loss :

= ⁷⁰⁄₂₅₀ ⋅ 100%

= ⁷⁄₂₅ ⋅ 100%

= 7 ⋅ 4%

= 28%

Problem 8 :

A car is travelling at 40 kilometers per hour. The car increases its speed to 56 kilometers per hour. Calculate the percentage increase in the speed of the car.

Solution :

Initial speed of car = 40 km. per hour

Increased speed = 56 km. per hour

Increase in speed :

= 56 - 40

= 16 km. per hour

Percentage increase in speed of the car :

= ¹⁶⁄₄₀ ⋅ 100%

= ⅖ ⋅ 100%

= 2 ⋅ 20%

= 40%

Problem 9 :

Susan buys an antique for $120 and sells it for $216. Work out her percentage profit.

Solution :

Cost price of an item = $120

Selling price of an item = $216

Selling price > Cost price ----> Profit

Profit = Sleeing price - Cost price

= 216 - 120

= $96

Percentage profit :

= ⁹⁶⁄₁₂₀ ⋅ 100%

= ⅘ ⋅ 100%

= 4 ⋅ 20%

= 80%

Problem 10 :

Holly bought a table for $80 She sold the table for $108 Find the percentage profit

Solution :

Cost price = $80

Selling price = $108

Selling price > Cost price ----> Profit

Profit = Selling price - Cost price

= 108 - 80

= 28

Percentage profit :

= ²⁸⁄₈₀ ⋅ 100%

= ⁷⁄₂₀ ⋅ 100%

= 7 ⋅ 5% 

= 35%

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.