PARALLEL LINES CUT BY A TRANSVERSAL

A transversal is a line that intersects two lines in the same plane at two different points.

In the diagram shown below, let the lines 'a' and 'b' be parallel. Because the line 't' cuts the lines 'a' and 'b', the line 't' is transversal.

So, the two parallel lines 'a' and 'b' cut by the transversal 't'.

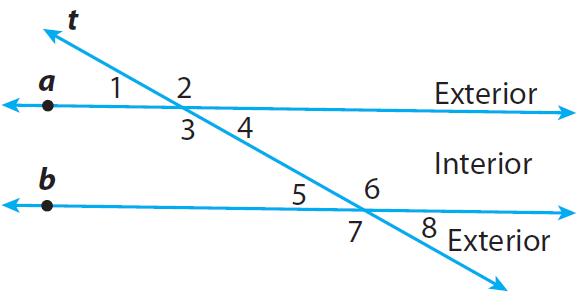
We can have the following important results from the above diagram.

Corresponding Angles :

Angles lie on the same side of the transversal t, on the same side of lines a and b.

Example : ∠ 1 and ∠ 5

Alternate Interior Angles :

Angles are nonadjacent angles that lie on opposite sides of the transversal t, between lines a and b.

Example : ∠ 3 and ∠ 6

Alternate Exterior Angles :

Angles lie on opposite sides of the transversal t, outside lines a and b.

Example : ∠ 1 and ∠ 8

Same-Side Interior Angles :

Angles lie on the same side of the transversal t, between lines a and b.

Example : ∠ 3 and ∠ 5

Reflect

Identify the pairs of angles in the diagram. Then make a conjecture about their angle measures.

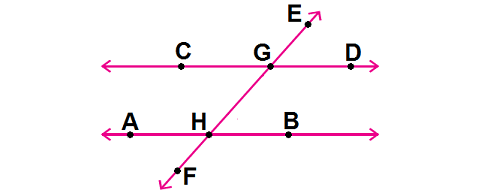
Corresponding Angles : 

∠CGE and ∠AHG, ∠DGE and ∠BHG, ∠CGH and ∠AHF, ∠DGH and ∠BHF ; congruent.

Alternate Interior Angles :

∠CGH and ∠BHG, ∠DGH and ∠AHG ; congruent.

Alternate Exterior Angles :

∠CGE and ∠BHF, ∠DGE and ∠AHF ; congruent.

Same-Side Interior Angles :

∠CGH and ∠AHG, ∠DGH and ∠BHG ; supplementary.

Solved Problems

Problem 1 :

In the figure given below,  let the lines l₁ and l₂ be parallel and m is transversal. If ∠F  =  65°, find the measure of each of the remaining angles.

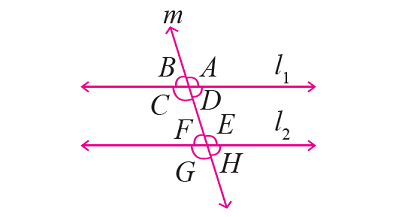
Solution :

From the given figure, 

∠F and ∠H are vertically opposite angles and they are equal. 

Then, ∠H  =  ∠F -------> ∠H  =  65°

∠H and ∠D are corresponding angles and they are equal. 

Then, ∠D  =  ∠H -------> ∠D  =  65°

∠D and ∠B are vertically opposite angles and they are equal. 

Then, ∠B  =  ∠D -------> ∠B  =  65°

∠F and ∠E are together form a straight angle.

Then, we have

∠F + ∠E  =  180°

Plug ∠F  =  65°

∠F + ∠E  =  180°

65° + ∠E  =  180°

∠E  =  115°

∠E and ∠G are vertically opposite angles and they are equal. 

Then, ∠G  =  ∠E -------> ∠G  =  115°

∠G and ∠C are corresponding angles and they are equal. 

Then, ∠C  =  ∠G -------> ∠C  =  115°

∠C and ∠A are vertically opposite angles and they are equal. 

Then, ∠A  =  ∠C -------> ∠A  =  115°

Therefore, 

∠A  =  ∠C  =  ∠E  =  ∠G  =  115°

∠B  =  ∠D  =  ∠F  =  ∠H  =  65°

Problem 2 :

In the figure given below,  let the lines l₁ and l₂ be parallel and t is transversal. Find the value of x.

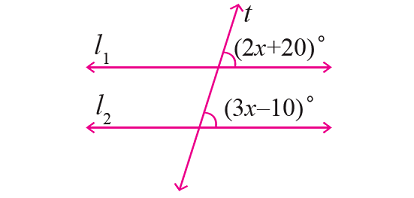
Solution :

From the given figure, 

∠(2x + 20)° and ∠(3x - 10)° are corresponding angles. 

So, they are equal. 

Then, we have

(2x + 20)°  =  ∠(3x - 10)°

2x + 20  =  3x - 10

Subtract 2x from each side. 

20  =  x - 10

Add 10 to each side. 

30  =  x

Problem 3 :

In the figure given below,  let the lines l₁ and l₂ be parallel and t is transversal. Find the value of x.

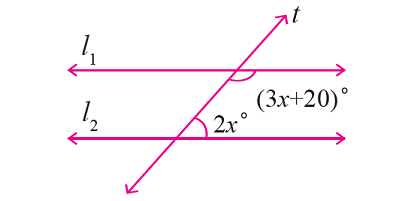
Solution :

From the given figure, 

∠(3x + 20)° and ∠2x° are consecutive interior angles. 

So, they are supplementary. 

Then, we have

(3x + 20)° + 2x°  =  180°

3x + 20 + 2x  =  180

Simplify.

5x + 20  =  180

Subtract 20 from each side.

5x  =  160

Divide each side by 8.

x  =  32

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.