HOW TO SHOW TWO CIRCLES ARE ORTHOGONAL
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Two circles are said to be orthogonal circles, if the tangent at their point of intersection are at right angles.
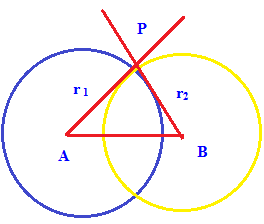
If two circles are cut orthogonally then it must satisfy the following condition.
2 g1 g2 + 2 f1 f2 = c1 + c2
General equation of circle :
x2 + y2 + 2gx + 2fy + c = 0
Example 1 :
Show that the circles
x2 + y2 - 8x + 6y - 23 = 0
and
x2 + y2 - 2x - 5y + 16 = 0
are orthogonal.
Solution :
From 1st equation :
x2 + y2 - 8x + 6y - 23 = 0
x2 + y2 + 2g1x + 2f1y + c1 = 0
2g1 = -8, g1 = -4
2f1 = 6, f1 = 3
and c1 = -2
From 2nd equation :
x2 + y2 - 2x - 5y + 16 = 0
2g2 = -2, g2 = -1
2f2 = -5, f2 = -5/2
and c2 = 16
Condition to prove two circles are orthogonal :
2 g1 g2 + 2 f1 f2 = c1 + c2
2(-4)(-1)+2(3)(-5/2) = -23+16
8-15 = -7
- 7 = -7
The two circles cut orthogonally and hence they are orthogonal circles.
Example 2 :
Show that the circles
x2 + y2 - 8x + 6y + 21 = 0
and
x2 + y2 - 2y - 15 = 0
are orthogonal.
Solution :
From 1st equation :
x2 + y2 - 8x + 6y + 21 = 0
x2 + y2 + 2g1x + 2f1y + c1 = 0
2g1 = -8, g1 = -4
2f1 = 6, f1 = 3
and c1 = 21
From 2nd equation :
x2 + y2 - 2y - 15 = 0
x2 + y2 + 2g2x + 2f2y + c2 = 0
2g1 = 0, g1 = 0
2f1 = -2, f1 = -1
and c1 = -15
2 (-4) (0) + 2 (-3) (-1) = 21 - 15
Condition to prove two circles are orthogonal :
2 g1 g2 + 2 f1 f2 = c1 + c2
2(-4)(0)+2(-3)(-1) = 21-15
0+6 = 6
6 = 6
The two circles cut orthogonally and hence they are orthogonal circles.
Example 3 :
Find the equation of the circle which passes through the point (1, 2) and cuts orthogonally each of the circles
x2 + y2 = 9
and
x2 + y2 − 2x + 8y − 7 = 0
Solution :
Let the required equation of the circle be
x2 + y2 + 2gx + 2fy + c = 0 ------(1)
The point (1, 2) lies on the circle
1+4+2g+4f+c = 0
2g+4f+c = −5 -----(2)
The circle (1) cuts the circle x2 + y2 = 9 orthogonally.
2g1g2 + 2f1f2 = c1 + c2
2g(0) + 2f(0) = c − 9
c = 9 ---(3)
Again the circle (1) cuts
x2 + y2 − 2x + 8y − 7 = 0
orthogonally.
2g(− 1) + 2f(4) = c − 7
-2g + 8f = 9 − 7 = 2
−g + 4f = 1 -----(4)
(2) becomes 2g + 4f = − 14
g + 2f = − 7 ------(5)
(4) + (5) => 6f = − 6 ⇒ f = − 1
(5) => g − 2 = − 7 => g = − 5
The required equation of the circle is
x2 + y2 − 10x − 2y + 9 = 0
Example 4 :
A circle S passes through the point (0, 1) and is orthogonal to the circles (x - 1)2 + y2 = 16 and x2 + y2 = 1. Then
a) radius of S is 8 b) radius of S is 7
c) center of S is (-7, 1)
d) center of S is (-8, 1)
Solution :
Let the required equation of the circle be
x2 + y2 + 2gx + 2fy + c = 0 ------(1)
The point (0, 1) lies on the circle
0 + 1 + 2g(0) + 2f(1) + c = 0
1 + 2f + c = 0
2f + c = -1 -----(2)
The circle (1) cuts the circle
(x - 1)2 + y2 = 16
orthogonally,
x2 - 2x + 1 + y2 = 16
x2 + y2 - 2x + 1 - 16 = 0
x2 + y2 - 2x - 15 = 0
2g2 = -2, 2f2 = 0
g2 = -1, f2 = 0, c2 = -15
2g1g2 + 2f1f2 = c1 + c2
2g(-1) + 2f(0) = c − 15
-2g = c − 15
-2g - c = -15
2g + c = 15 -----(3)
The circle (1) cuts the circle
x2 + y2 = 1
orthogonally,
2g2 = 0, 2f2 = 0, c2 = -1
g2 = 0, f2 = 0, c2 = -1
2g1g2 + 2f1f2 = c1 + c2
2g(0) + 2f(0) = c − 1
c = 1
Applying the value of c in (3), we get
2g + 1 = 15
2g = 14
g = 7
Applying the values of g and c in (1), we get
x2 + y2 + 2(7)x + 2fy + 1 = 0
Since the required circle passes through the point (0, 1), we can apply.
02 + 12 + 2(7)(0) + 2f(1) + 1 = 0
1 + 2f + 1 = 0
2f = -2
f = -1
Applying into the equation, we get
x2 + y2 + 2(7)x + 2(-1)y + 1 = 0
x2 + y2 + 14x - 2y + 1 = 0
Center (-g, -f) ==> (-7, 1)
So, option c is correct.
Finding radius :
= √g2 + f2 - c
= √(-7)2 + 12 - 1
= 7
Then, option b is also correct.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
SAT Math Practice
Dec 05, 25 04:04 AM
SAT Math Practice - Different Topics - Concept - Formulas - Example problems with step by step explanation -
10 Hard SAT Math Questions (Part - 37)
Dec 03, 25 07:02 AM
10 Hard SAT Math Questions (Part - 37) -
Factorial Problems and Solutions
Dec 02, 25 09:27 AM
Factorial Problems and Solutions

