ORDERING REAL NUMBERS IN A REAL-WORLD CONTEXT

Calculations and estimations in the real world may differ. It can be important to know not only which are the most accurate but which give the greatest or least values, depending upon the context.

Example 1 : 

Four people have found the distance in kilometers across a canyon using different methods. Their results are given in the table. Order the distances from greatest to least.

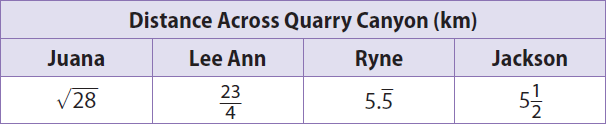
Solution : 

Step 1 :

Write each value as a decimal.

√28 is between 5.2 and 5.3

Since 5.3² = 28.09, an approximate value for √28 is 5.3. 

23/4  =  5.75

5.5 (bar above 5)  =  5.5555........

5 1/2  =  5.5

Step 2 : 

Plot √28, 23/4, 5.555..., 5 1/2 on a number line. 

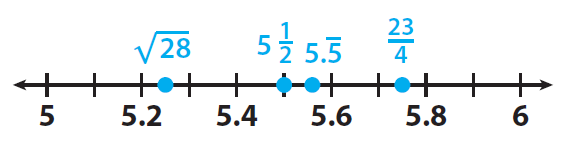
From greatest to least, the distances are :

23/4 km, 5.555.... km, 5 1/2 km, √28 km.

Example 2 : 

Six students (A, B, C, D, E and F) of grade 10 ran the following distances in kilometers in 2 hours.

4√2, 2√3, 3√2, √17, 3√3 and 5

Which student did run the farthest distance ? 

Order the students by distance covered by them from least to greatest. 

Solution : 

Key Concept :

Most of the given distances are irrational numbers.

So, square the given distances and order them from least to greatest.

Step 1 :

Take square to 4√2. 

(4√2)²  =  (4)²(√2)²

(4√2)²  =  (16)(2)

(4√2)²  =  32 -----(A)

Step 2 :

Take square to 2√3. 

(2√3)²  =  (2)²(√3)²

(2√3)²  =  (4)(3)

(2√3)²  =  12 -----(B)

Step 3 :

Take square to 3√2. 

(3√2)²  =  (3)²(√2)²

(3√2)²  =  (9)(2)

(3√2)²  =  18 -----(C)

Step 4 :

Take square to √17. 

(√17)²  =  17 -----(D)

Step 5 :

Take square to 3√3. 

(3√3)²  =  (3)²(√3)²

(3√3)²  =  (9)(3)

(3√3)²  =  27 -----(E)

Step 6 :

Take square to 5. 

(5)²  =  25 -----(F)

Step 7 :

Comparing (A), (B), (C), (D), (E) and (F), student A ran the farthest distance. 

And also, from (A), (B), (C), (D), (E) and (F), we can write the squares of the given distances from least to greatest as given below. 

12, 17, 18, 25, 27, 32

In the above order, write the corresponding distance  to its square to write the given distances in the order from least to greatest. 

2√3 km, √17 km, 3√2 km, 5 km, 3√3 km, 4√2 km

Hence, the order of the students by distance covered by them from least to greatest is

B, D, C, F, E, A

Your Turn

Question 1 : 

Four people have found the distance in miles across a crater using different methods. Their results are given below.

Jonathan : 10/3

Elaine : 3.4545...

Jose : 3 1/2

Lashonda : √10

Order the distances from greatest to least.

Question 2 : 

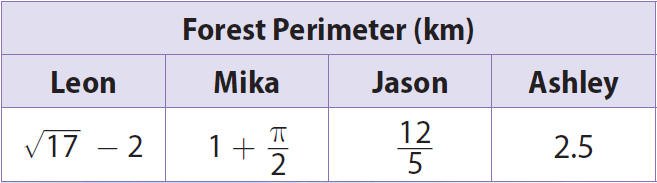
Four people have found the perimeter of a forest using different methods. Their results are given in the table. Order their calculations from greatest to least.

Answers for the above questions :

1)  3 1/2 mi, 3.4545... mi, 10/3 mi, √10 mi.

2)  1 + π/2 km, 2.5 km, 12/5 km, √17 - 2km.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.