ORDERING RATIONAL AND IRRATIONAL NUMBERS

Example 1 : 

Order √22, (π + 1) and 4½ from least to greatest. Then graph them on the number line.

Solution :

Step 1 :

First approximate √22.

√22 is between 4 and 5. Since we don’t know where it falls between 4 and 5, we need to find a better estimate for √22. 

So that we can compare it to 4½.

Since 22 is closer to 25 than 16, use squares of numbers between 4.5 and 5 to find a better estimate of √22. 

4.5² = 20.25

4.6² = 21.16

4.7² = 22.09

4.8² = 23.04

Since 4.7² = 22.09, an approximate value for √22 is 4.7.

That is, 

 √22 ≈ 4.7 ----(1)

Step 2 :

An approximate value of π is 3.14. So an approximate value of π+1 is 4.14.

That is, 

π + 1 ≈ 4.14 ----(2)

Step 3 :

The value of 4½ is 4.5. 

That is, 

4½ = 4.5 ----(3)

Step 4 :

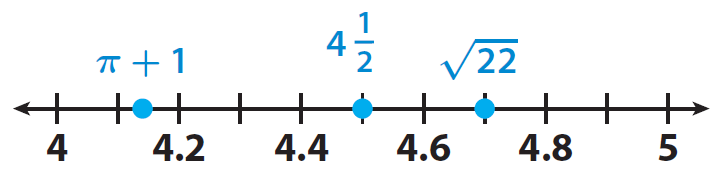
Comparing (1), (2) and (3), we can order the numbers from least to greatest as given below. 

π + 1, 4½ and √22

Step 5 :

Read the numbers from left to right to place them on a number line in order from least to greatest.

Example 2 : 

Order 4√2, 2√3, 3√2, √17, 3√3 and 5 from least to greatest. 

Solution :

Key Concept :

Most of the given real numbers are irrational numbers.

So, square the given real numbers and order them from least to greatest.

Step 1 :

Take square to the number 4√2. 

(4√2)² = (4)²(√2)²

(4√2)² = (16)(2)

(4√2)² = 32 ----(1)

Step 2 :

Take square to the number 2√3. 

(2√3)² = (2)²(√3)²

(2√3)² = (4)(3)

(2√3)² = 12 ----(2)

Step 3 :

Take square to the number 3√2. 

(3√2)² = (3)²(√2)²

(3√2)² = (9)(2)

(3√2)² = 18 ----(3)

Step 4 :

Take square to the number √17. 

(√17)² = 17 ----(4)

Step 5 :

Take square to the number 3√3. 

(3√3)² = (3)²(√3)²

(3√3)² = (9)(3)

(3√3)² = 27 -----(5)

Step 6 :

Take square to the number 5. 

(5)² = 25 ----(6)

Step 7 :

Comparing (1), (2), (3), (4), and (6), we can write the squares of the given irrational numbers from least to greatest as given below. 

12, 17, 18, 25, 27, 32

In the above order, write the corresponding real number to its square to write the given real numbers in the order from least to greatest. 

2√3, √17, 3√2, 5, 3√3, 4√2

Example 3 :

Order 2, √5, 6^1/3, 4^2/3 from least to greatest

Solution :

Step 1 :

First convert the radical in √5 as exponent. 

Then, we have

√5 = 5^1/2

Step 2 :

Now, the given numbers are

2, 5^1/2, 6^1/3, 4^2/3

In the numbers listed above, we find the exponents 1/2, 1/3 and 2/3. 

All the exponents are fractions and the denominators of the fractions are 2 and 3. 

The least common multiple of the denominators 2 and 3 is 6

Step 3 : 

Now take exponent 6 to all of the numbers in step 2.

2⁶, (5^1/2)⁶, (6^1/3)⁶, (4^2/3)⁶

Simplify.

2⁶, 5³, 6², 4⁴

64, 125, 36, 256

Step 4 :

Order the numbers from least to greatest. 

36, 64, 125, 256

Step 5 :

Using the order of numbers in step 4, write the given rational and irrational numbers in the order from least to greatest. 

6^1/3, 2, √5, 4^2/3

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.