ORDER OF OPERATIONS WITH FRACTIONS

Example 1 :

2/3 + 3/4 x 2/3

Solution :

= 2/3 + 3/4 x 2/3

= 2/3 + 1/2

= (4 + 3)/6

= 7/6

Example 2 :

3/5 – 5/2 x 4/3

Solution :

= 3/5 – 5/2 x 4/3

= 3/5 – 10/3

= (9 - 50)/15

= -41/15

Example 3 :

3/5 x 1/3 + 2/3 x 1/4

Solution :

= 3/5 x 1/3 + 2/3 x 1/4

= 1/5 + 1/6

= (6 + 5)/30

= 11/30

Example 4 :

4/3 x 1/2 – 1/6 x 2/3

Solution :

= 4/3 x 1/2 – 1/6 x 2/3

= 2/3 – 1/9

= (6 - 1)/9

= 5/9

Example 5 :

(2/3)² – 3/4 x 1⅔

Solution :

= (2/3)² – 3/4 x 1⅔

=  4/9 – 3/4 x 5/3

= 4/9 – 5/4

= (16 - 45)/36

= -29/36

Example 6 :

4 x 1⅓ – 5 x 2/7

Solution :

= 4 x 1⅓ – 5 x 2/7

= 4 x 4/3 – 5 x 2/7

= 16/3 - 10/7

= (112 - 30)/21

= 82/21

Example 7 :

2/3 – 3/2 ÷ 4/5

Solution :

= 2/3 – 3/2 ÷ 4/5

= 2/3 – 3/2 x 5/4

= 2/3 – 15/8

= (16 - 45)/24

= -29/24

Example 8 :

5/3 ÷ 1/2 + 4/3

Solution :

= 5/3 ÷ 1/2 + 4/3

= 5/3 x 2/1 + 4/3

= 10/3 + 4/3

= (10 + 4)/3

= 14/3

Example 9 :

1/2 x 2/5 – 3/4 ÷ 6/5

Solution :

= 1/2 x 2/5 – 3/4 ÷ 6/5

1/2 x 2/5 – 3/4 x 5/6

= 1/5 – 5/8

= (8 - 25)/40

= -17/40

Example 10 :

2/5 ÷ (-1/2) + 3/4 x 2/5

Solution :

= 2/5 ÷ (-1/2) + 3/4 x 2/5

= 2/5 x (-2/1) + 3/4 x 2/5

= -4/5 + 6/20

= (-16 + 6)/20

= -10/20

= -1/2 

Without finding the product, copy and complete the statement using <, >, or =. Explain your reasoning.

Example 11 :

4/7  ____ (9/10 x 4/7)

Solution :

4/7  ____ (9/10 x 4/7)

R.H.S

= 9/10 x 4/7

= (9 x 4)/(10 x 7)

= 36/70

To compare two fractions, it should be like fractions. To have same denominator, we have to multiply both numerator and denominator by 10.

= (4/7) x (10/10)

= 40/70

Comparing the fractions 40/70 and 36/70, 40/70 is greater. Then 

4/7  > (9/10 x 4/7)

Example 12 :

(5/8 x 22/15)  ____ 5/8

Solution :

(5/8 x 22/15)  ____ 5/8

L.H.S

= 5/8 x 22/15

= (5 x 22)/(8 x 15)

= 110/120

Multiplying both numerator and denominator of 5/8 by 15, we get

= (5/8) x (15/15)

= 75/120

Comparing the fractions 110/120 and 75/120, 110/120 is greater fraction. Then,

(5/8 x 22/15) > 5/8

Example 13 :

5/6  ____ (5/6 x 7/8)

Solution :

5/6  ____ (5/6 x 7/8)

R.H.S

= 5/6 x 7/8

= 35/48

To make the denominators same, we have to multiply numerator and denominator of 5/6 by 8.

= (5/6) x (8/8)

= 40/48

Comparing these two fractions 40/48 and 35/48, 40/48 is greater.

5/6 < (5/6 x 7/8)

Example 14 :

Three pictures hang side by side on a wall. What is the total area of the wall that the pictures cover ?

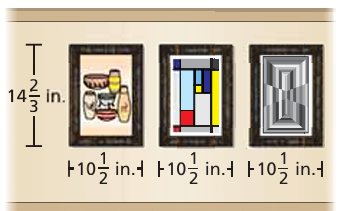
Solution :

Each pictures is in the shape of rectangle.

Length = 14  2/3 inches

Width = 10  1/2 inches

Area of rectangle = length x width

= 14  2/3 x 10  1/2

= 44/3 x 21/2

= 22 x 7

= 154 square inches.

Area covered by one hanging is 154 suqare inches

Example 17 :

A certain small factory employs 98 workers. Of these, 10 receive a wage of $150 per day and the rest receive $85.50 per day. To the management, a week is equal to 6 working days. How much does the factory pay out for each week?

Solution :

Number of employs = 98

Number of workers who recieve $150 per day = 10

Number of workers who recives $85.50 per day = 98 - 10

= 88

Number of days working = 6

Amount paid by the factory for each week

= 10(150) + 88(85.50)

= 1500 + 7524

= 9024

So, the amount paid by the factory for 6 days of work is $9024.

Example 18 :

Emily had 30 cookies to bring to school for her birthday. Three students wanted two cookies each. Then, a new student came to the school that day and he wanted three cookies. Then, one of the three kids gave their two cookies back. Emily was still passing out cookies. How many cookies did Emily have left to pass out after the students gave theirs back?

Solution :

Number of cookies she have left to pass out

= 30 - [3(2) + 2 - 2]

= 30 - [6 + 2 - 2]

= 30  - 6

= 24 cookies

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.