ORDER OF OPERATIONS USING PEMDAS WORKSHEET

Problem 1 :

a)  (5 - 2)² - 6

b)  3 × 4 + 5²

c)  4 × 3² - (3 + 2)²

d)  3 - 2² ÷ 2 + 1

e)  (5 - 2)² - 2²

f)  (15 - 3²) ÷ 3

g)  5 × 2² + 2 × 3²

h)  5 × (2² + 2) + 6

i)  35 - 3 × 2³ + 7

Solution :

a)

b)

c)

d)

e)

f)

g)

h)

i)

Problem 2 :

Replace * with either +, -, ×, ÷ or ÷ to make a true statement :

a)  (18 * 2) ÷ 10 = 2

b)  (10 * 3) * 7 = 1

c)  15 * 3 + 2 * 5 = 15

Solution :

a)

 (18 * 2) ÷ 10 = 2

By replacing * as +, we get

(18 + 2) ÷ 10 = 2

20 ÷ 10 = 2

2 = 2 (true)

b)

(10 * 3) * 7 = 1

By replacing * as -, we get

(10 - 3) * 7 = 1

7 * 7 = 1

By replacing * as ÷, we get

7 ÷ 7 = 1

1 = 1 (true)

c)

 15 * 3 + 2 * 5 = 15

By replacing * as ÷, we get

 15 ÷ 3 + 2 * 5 = 15

5 + 2 * 5 = 15

By replacing * as ×, we get

5 + 2 × 5 = 15

5 + 10 = 15

15 = 15 (true)

Problem 3 :

Insert brackets into the following to make them true :

a)  8 + 4 ÷ 2 + 2 = 3

b)  5 + 3 × 6 - 10 = 38

c)  13 + 5 ÷ 5 + 4 = 2

Solution :

a)

8 + 4 ÷ 2 + 2 = 3

(8 + 4) ÷ (2 + 2) = 3

12 ÷ 4 = 3

3 = 3 (true)

b)

5 + 3 × 6 - 10 = 38

  (5 + 3) × 6 - 10 = 38

8 × 6 - 10 = 38

48 - 10 = 38

38 = 38 (true)

c)

13 + 5 ÷ 5 + 4 = 2

(13 + 5) ÷ (5 + 4) = 2

18 ÷ 9 = 2

2 = 2 (true)

Problem 4 :

A woman has $255 in her purse. She gives $35 to each of her five children. How much money does she have left?

Solution :

Amount she has left in her purse 

Amount given for each children = $35

Number of children they get = 5

Amount she have left = 255 - (35 x 5)

= 255 - 175

= 80

Problem 5 :

The equation shown in the table can be used to find the output when the input is 2, 4, and 6.

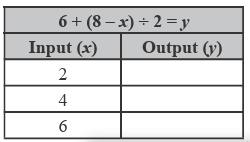
Which numbers complete the table?

a)  6, 5, 4      b)    8, 9, 10        c) 9, 8, 7      d)  14, 12, 10

Solution :

When x = 2

y = 6 + (8 - x) ÷ 2

Applying x = 2, we get

y = 6 + (8 - 2) ÷ 2

= 6 + 6 ÷ 2

= 6 + 3

= 9

When x = 4

y = 6 + (8 - x) ÷ 2

Applying x = 4, we get

y = 6 + (8 - 4) ÷ 2

= 6 + 4 ÷ 2

= 6 + 2

= 8

When x = 6

y = 6 + (8 - x) ÷ 2

Applying x = 6, we get

y = 6 + (8 - 6) ÷ 2

= 6 + 2 ÷ 2

= 6 + 1

= 7

Problem 6 :

Using Order of Operations (PEMDAS) solve the expression.

(4 + 20) ÷ 2 + 6

a) 4     b) 3    c) 18     d) 10

Solution :

= (4 + 20) ÷ 2 + 6

First simplify the bracket.

= 24 ÷ 2 + 6

= 12 + 6

= 18

So, option c is correct.

Problem 7 :

Find the value of y, when x = 4

(x + 4) x 5 = y

a) 4     b) 35     c) 24     d) 40

Solution :

Applying x = 4, we get

y = (4 + 4) x 5

= 8 x 5

= 40

So, option d is correct.

Problem 8 :

Davi has 5 times as many hats as Kwan. Davi has 20 hats. Which can be used to find the number of hats Kwan has?

a) 5 + h = 20; h = 15      b) 5 × h = 20; h = 4

c) 5 × 20 = h; h = 100     d) 5 + 20 = h; h = 25

Solution :

Let k be the number of hats Kwan has.

5 x k = number of hats Davi has

Which is option c is correct.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.