OPTIMIZATION PROBLEMS INVOLVING POLYNOMIAL FUNCTIONS

Problem 1 :

A cylindrical can with closed bottom and closed top is to be constructed to have a volume of one gallon (approximately 231 cubic inches). The material used to make the bottom and top costs $0.06 per square inch, and the material used to make the curved surface costs $0.03 per square inch. Find the radius and height of the can that minimize the total cost, and determine what that minimum cost is.

Solution :

Let r and h be the radius and height of the cylindrical can respectively.

Surface area of the cylindrical can  =  2πr² + 2πrh

Volume of cuboid  =  πr² h

πr² h  =  231

(22/7) ⋅ r²⋅ h  =  231

r² h  =  231 ⋅ (7/22)

r² h  =  10.5

h  =  10.5/r²

s(r)  =  2πr² + 2πr(10.5/r²)

s(r)  =  2πr² + 21π/r

The material used to make the bottom and top costs $0.06 per square inch, and the material used to make the curved surface costs $0.03 per square inch.

Cost of the function  =  0.06 (2πr²) + 0.03(21π/r)

s(r)  =  0.12πr² + (0.63π/r)

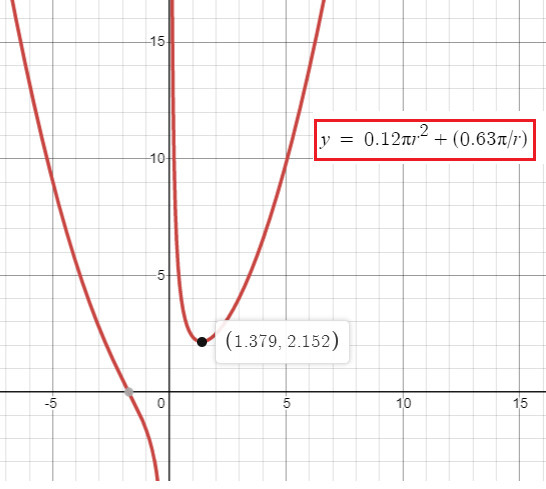
Minimum value is 1.379

r  =  1.379

h  =  10.5/r²

h  =  10.5/(1.379)²

h  =  5.52

Minimum cost  =  0.12π(1.379)² + (0.63π/1.379)

=  0.716 + 1.434

=  2.15

Problem 2 :

A rancher has 180 feet of fencing with which to enclose four adjacent rectangular corrals as shown. What dimensions should be used so that the enclosed area will be a maximum? What will the area be

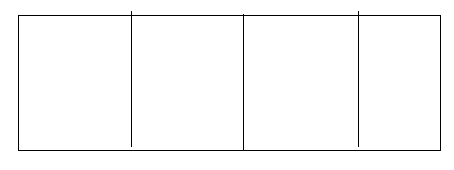
Solution :

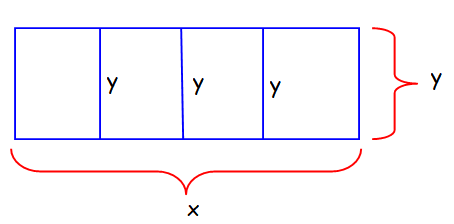
Let x and y be the length and width of the rectangle.

Perimeter of the rectangular field  =  180 feet

2x + 5y  =  180

5y  =  180 - 2x

y  =  (180 - 2x)/5

Area of rectangular field  =  xy

A(x)  =  x((180 - 2x)/5)

Domain : 

0 < x < 90

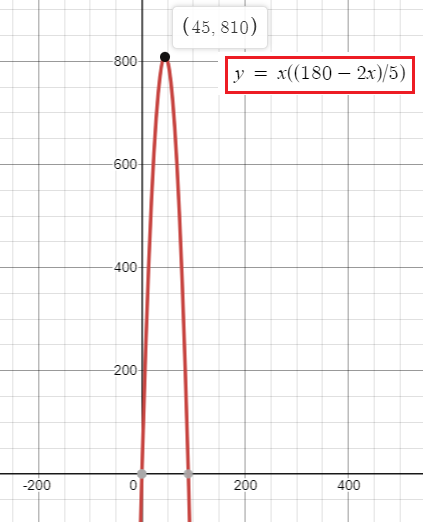
Minimum value of x is 45.

To get the value of y, we apply the value of x in

y  =  (180 - 2x)/5

y  =  (180 - 2(45))/5

y  =  (180 - 90)/5

y  =  18

Minimum area  =  45((180 - 2(45))/5)

=  45 (180 - 90)/5

=  9(90)

=  810 square feet.

Hence the minimum area if 810 square feet.

Problem 3 :

A rectangle is bounded by the x-axis and the semicircle

y  =  √(25 - x²)

as shown. What length and width should the rectangle have so that its area is a maximum?

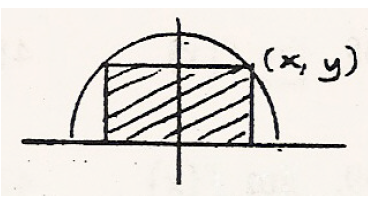
Solution :

From the picture given above, length of the rectangle is 2x and width of the rectangle is y.

Area of rectangle  =  2xy

A(x)  =  2x(√(25 - x²))

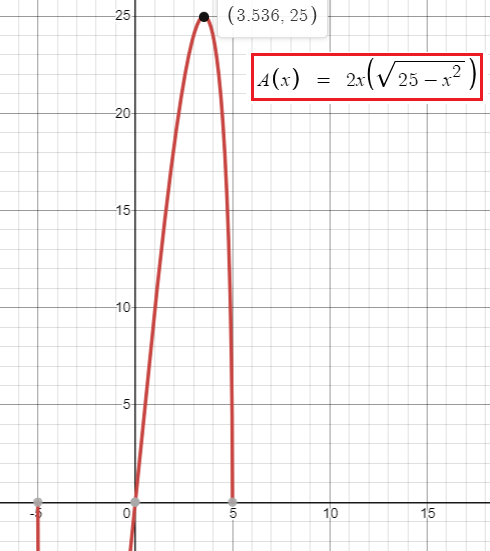
x is 3.536

To find the value of y, we apply

y  =  √(25 - (3.53)²)

y  =  √(25 - (3.53)²)

y  =  3.54

So, its maximum area is 25.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.