OPPOSITE ANGLES OF A CYCLIC QUADRILATERAL ARE SUPPLEMENTARY
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
A quadrilateral is called cyclic quadrilateral if all its four vertices lie on the circumference of the circle. Now we are going to learn the special property of cyclic quadrilateral.
Theorem :
Opposite angles of a cyclic quadrilateral are supplementary.
Proof :
Consider the quadrilateral ABCD whose vertices lie on a circle. We want to show that its opposite angles are supplementary.
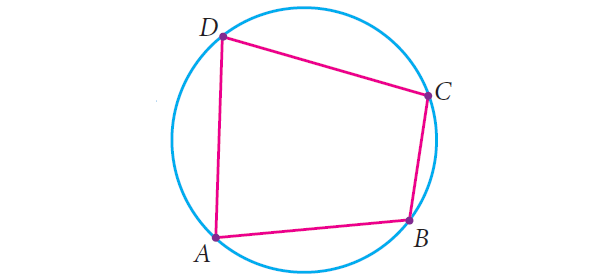
Connect the center O of the circle with each vertex. You now see four radii OA, OB, OC and OD giving rise to four isosceles triangles OAB, OBC, OCD and ODA.
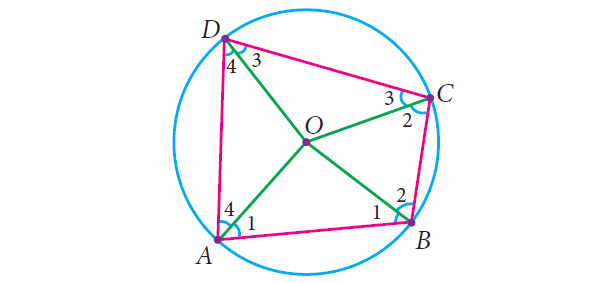
The sum of the angles around the center of the circle is 360°. The angle sum of each isosceles triangle is 180°.
2(∠1 + ∠2 + ∠3 + ∠4) + Angle at center O = 4 ⋅ 180°
2(∠1 + ∠2 + ∠3 + ∠4) + 360° = 720°
Subtract 360° from each side.
2(∠1 + ∠2 + ∠3 + ∠4) = 360°
Divide each side by 2.
∠1 + ∠2 + ∠3 + ∠4 = 180°
You now interpret this as
|
(i) (∠1 + ∠2) + (∠3 + ∠4) = 180° |
(sum of opposite angles B and D) |
|
(i) (∠1 + ∠4) + (∠2 + ∠3) = 180° |
(sum of opposite angles A and C) |
Converse of the Theorem :
If a pair of opposite angles of a quadrilateral is supplementary, then the quadrilateral is cyclic.
Example 1 :
In the diagram shown below. ABCD is a cyclic quadrilateral in which ∠BCD = 100° and ∠ABD = 50°. Find ∠ADB.
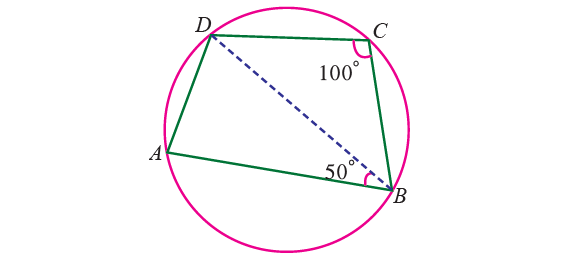
Solution :
By Theorem,
∠BAD + ∠BCD = 180°
Substitute ∠BCD = 100°.
∠BAD + 100° = 180°
Subtract 100° from each side.
∠BAD = 80°
In triangle ABD,
∠ABD + ∠BAD + ∠ADB = 180°
50° + 80° + ∠ADB = 180°
130° + ∠ADB = 180°
Subtract 130° from each side.
∠ADB = 50°
Example 2 :
In the diagram shown below, ABCD is a cyclic quadrilateral whose diagonals intersect at P such that ∠CBD = 30° and ∠BAC = 50°. Find ∠CAD and ∠BCD.
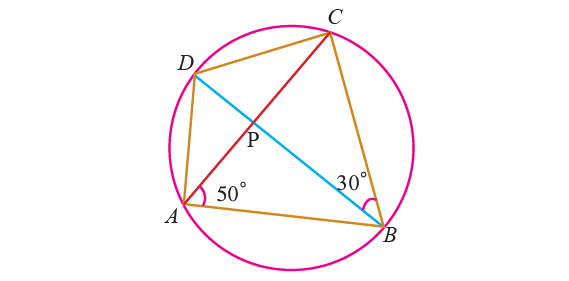
Solution :
∠CAD :
The angles at the circumference subtended by the same arc are equal. ∠CAD and ∠CBD at the circumference subtended by the same arc CD.
∠CAD = ∠CBD
∠CAD = 30°
∠BCD :
By Theorem,
∠BAD + ∠BCD = 180°
In the above diagram, ∠BAD = ∠BAC + ∠CAD.
(∠BAC + ∠CAD) + ∠BCD = 180°
∠BAC + ∠CAD + ∠BCD = 180°
Substitute ∠BAC = 50° and ∠CAD = 30°.
50° + 30° + ∠BCD = 180°
80° + ∠BCD = 180°
Subtract 80° from each side.
∠BCD = 100°
Example 3 :
In the diagram shown below, O is the center of the circle and ∠ADC = 120°. Find the value of x.
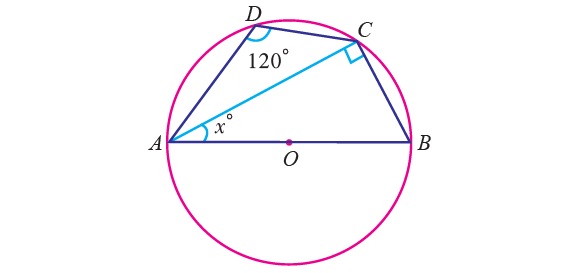
Solution :
By Theorem,
∠ABC + ∠ADC = 180°
Substitute ∠ADC = 120°.
∠ABC + 120° = 180°
Subtract 120° from each side.
∠ABC = 60°
∠ACD = 90° (angle in a semi circle is a right angle)
In triangle ABC,
∠BAC + ∠ACB + ∠ABC = 180°
x° + 90° + 60° = 180°
x + 90 + 60 = 180
x + 150 = 180
Subtract 150 from each side.
x = 30
Example 4 :
In the figure given below, ABCD is a cyclic quadrilateral in which AB || DC. If ∠BAD = 100° find ∠BCD, ∠ADC and ∠ABC.
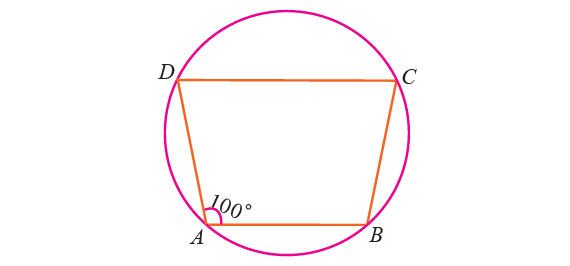
Solution :
∠BCD :
By Theorem,
∠BAC + ∠BCD = 180°
Substitute ∠BAD = 100°.
100° + ∠BCD = 180°
Subtract 100° from each side.
∠BCD = 80°
∠ADC :
Since AB || DC, AD is transversal.
When two parallel lines intersected by a transversal, same side interior angles are supplementary.
∠BAD + ∠ADC = 180°
Substitute ∠BAD = 100°.
100° + ∠ADC = 180°
Subtract 100° from each side.
∠ADC = 80°
∠ABC :
By Theorem,
∠ABC + ∠ADC = 180°
Substitute ∠ADC = 80°.
∠ABC + 80° = 180°
Subtract 80° from each side.
∠ABC = 100°
Example 5 :
In the diagram shown below, PQ is a diameter of a circle with center O. If ∠PQR = 55°, ∠SPR = 25° and ∠PQM = 50°. Find ∠QPR, ∠QPM and ∠PRS.
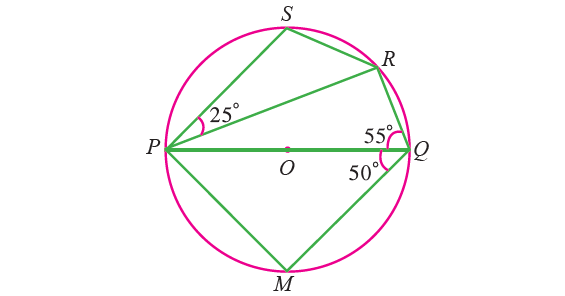
Solution :
∠QPR :
∠PRQ = 90° (angle in a semi circle is a right angle)
In triangle PRQ,
∠PRQ + ∠QPR + ∠PQR = 180°
90° + ∠QPR + 55° = 180°
∠QPR + 145° = 180°
Subtract 145° from each side.
∠QPR = 35°
∠QPM :
In triangle QPM,
∠QPM + ∠MQP + ∠QMP = 180°
∠QPM + 50° + 90° = 180°
∠QPM + 140° = 180°
Subtract 140° from each side.
∠QPM = 40°
∠PRS :
By Theorem,
∠PQR + ∠PSR = 180°
55° + ∠PSR = 180°
Subtract 55° from each side.
∠PSR = 125°
In triangle PSR,
∠PSR + ∠SPR + ∠PRS = 180°
125° + 25° + ∠PRS = 180°
150° + ∠PRS = 180°
Subtract 150° from each side.
∠PRS = 30°
Example 6 :
Find the values of x and y.
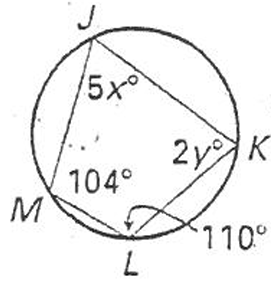
Solution :
Sum of opposite angles = 180
|
104 + 2y = 180 2y = 180 - 104 2y = 76 y = 76/2 y = 38 |
110 + 5x = 180 5x = 180 - 110 5x = 70 x = 70/5 x = 14 |
So, the values of x and y are 14 and 38 respectively.
Example 7 :
Find the values of x and y.
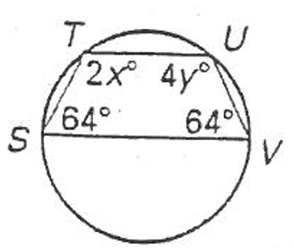
Solution :
Sum of opposite angles = 180
|
64 + 4y = 180 4y = 180 - 64 4y = 116 y = 116/4 y = 29 |
64 + 2x = 180 2x = 180 - 64 2x = 116 x = 116/2 x = 58 |
So, the values of x and y are 58 and 29 respectively.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 1)
Feb 05, 26 09:37 AM
Digital SAT Math Problems and Solutions (Part - 1) -
AP Precalculus Problems and Solutions
Feb 05, 26 06:41 AM
AP Precalculus Problems and Solutions -
SAT Math Preparation with Hard Questions
Feb 05, 26 05:30 AM
SAT Math Preparation with Hard Questions

