OPPOSITE ANGLES OF A CYCLIC QUADRILATERAL ARE SUPPLEMENTARY PROOF

Theorem :

Opposite angles of a cyclic quadrilateral are supplementary (or) The sum of opposite angles of a cyclic quadrilateral is 180°.

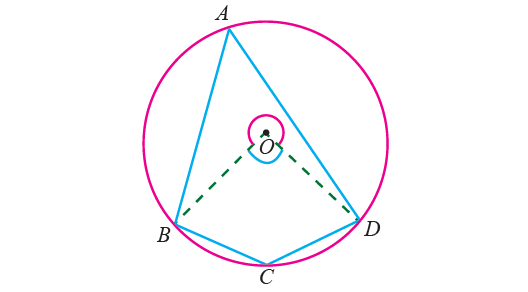
Given : O is the center of circle. ABCD is the cyclic quadrilateral.

To prove : ∠BAD + ∠BCD = 180°, ∠ABC + ∠ADC = 180°.

Construction : Join OB and OD.

Proof :

(i) ∠BAD = (1/2)∠BOD.

(The angle subtended by an arc at the center is double the angle on the circle)

(ii) ∠BCD = (1/2) reflex ∠BOD.

(iii) ∠BAD + ∠BCD = (1/2)∠BOD + (1/2) reflex ∠BOD.

Add (i) and (ii).

∠BAD + ∠BCD = (1/2)(∠BOD + reflex ∠BOD)

∠BAD + ∠BCD = (1/2) ⋅ (360°)

(Complete angle at the center is 360°)

∠BAD + ∠BCD  =  180°

(iv) Similarly ∠ABC + ∠ADC  =  180°.

Problem 1 :

In the figure given below, O is the center of a circle and ∠ADC = 120°. Find the value of x.

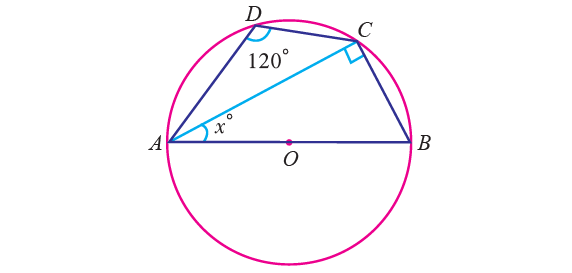
Solution :

ABCD is a cyclic quadrilateral. we have

∠ABC + ∠ADC = 180°

Substitute ∠ADC = 120°.

∠ABC + 120° = 180°

Subtract 120° from both sides.

∠ABC = 60°

Also ∠ACB = 90° (angle on a semi circle).

In triangle ABC we have,

∠BAC + ∠ACB + ∠ABC = 180°

Substitute ∠ACB = 90° and ∠ABC = 60°.

∠BAC + 90° + 60° = 180°

∠BAC + 150° = 180°

Subtract 150° from both sides.

∠BAC = 30°

So, the value of x is 30.

Problem 2 :

In the figure given below, ABCD is a cyclic quadrilateral in which AB || DC. If ∠BAD = 100° find

(i) ∠BCD

(ii) ∠ADC

(iii) ∠ABC

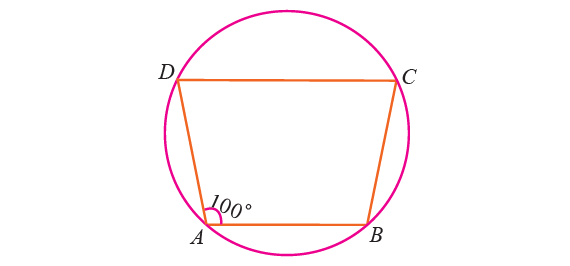
Solution :

(i) ∠BCD :

∠BAD + ∠BCD = 180°

Substitute ∠BAD = 100°.

100° + ∠BCD = 180°

Subtract 100° from both sides.

∠BCD = 80°

(ii) ∠ADC :

Because AB || DC and AD is transversal,

∠BAD + ∠ADC = 180°

Substitute ∠BAD = 100°.

100° + ∠ADC = 180°

Subtract 100° from each side.

∠ADC = 80°

(iii) ∠ABC :

∠ADC + ∠ABC = 180°

Substitute ∠ADC = 80°.

80° + ∠ABC = 180°

Subtract 80° from both sides.

∠ABC = 100°

Problem 3 :

In the figure given below, ABCD is a cyclic quadrilateral in which ∠BCD = 100° and ∠ABD = 50° find ∠ADB. 

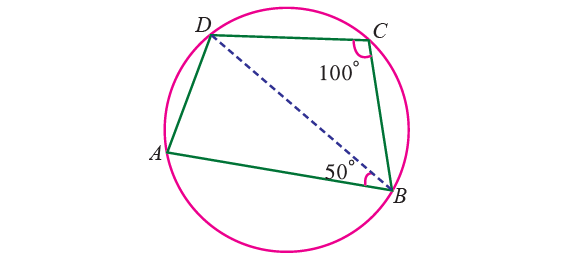
Solution :

∠DAB + ∠DCB = 180°

Substitute ∠DCB = 100°.

∠DAB + 100° = 180°

Subtract 100° from both sides.

∠DAB = 80°

In triangle ADB,

∠DAB + ∠ABD + ∠ADB = 180°

Substitute ∠DAB = 80° and ∠ABD = 50°.

80° + 50° + ∠ADB = 180°

130° + ∠ADB = 180°

Subtract 130° from both sides.

∠ADB = 180°

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.