OPPOSITE ANGLES IN A CYCLIC QUADRILATERAL WORKSHEET

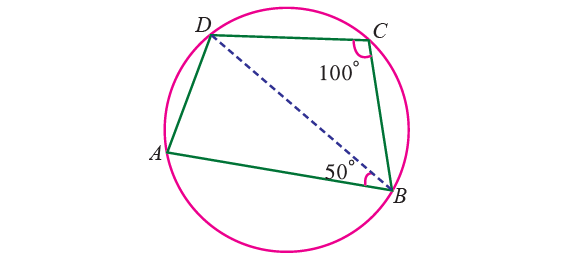
1. In the diagram shown below. ABCD is a cyclic quadrilateral in which ∠BCD = 100° and ∠ABD = 50°. Find ∠ADB.

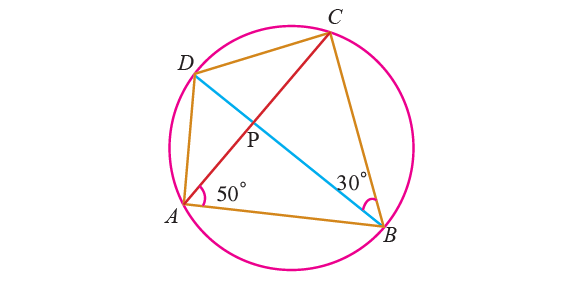
2. In the diagram shown below, ABCD is a cyclic quadrilateral whose diagonals intersect at P such that ∠CBD = 30° and ∠BAC = 50°. Find ∠CAD and ∠BCD.

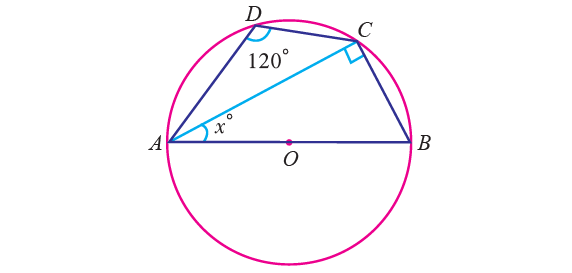
3. In the diagram shown below, O is the center of the circle and ∠ADC = 120°. Find the value of x.

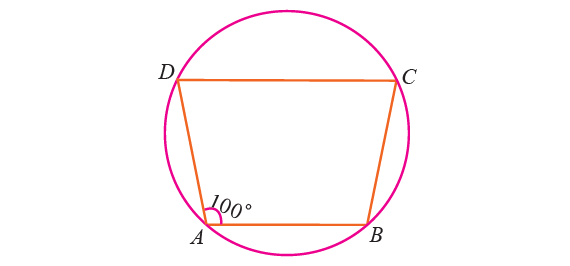
4. In the figure given below, ABCD is a cyclic quadrilateral in which AB || DC. If ∠BAD = 100° find ∠BCD, ∠ADC and ∠ABC.

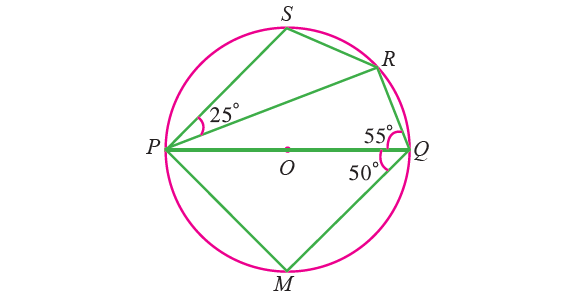
5. In the diagram shown below, PQ is a diameter of a circle with center O. If ∠PQR = 55°, ∠SPR = 25° and ∠PQM = 50°. Find ∠QPR, ∠QPM and ∠PRS.

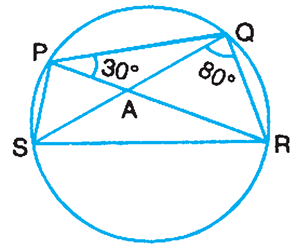
6. In the figure  PQRS is a cyclic quadrilateral whose diagonals intersect at A. If ∠SQR = 80^o and ∠QPR = 30^o, find ∠SRQ.

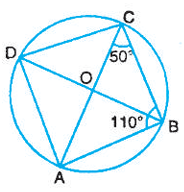
7.  In the figure, ABCD is a cyclic quadrilateral whose diagonals intersect at O. If ∠ACB = 50^o and ∠ABC = 110^o, find ∠BDC.

8. Given <ADC = 80. The measure of <CBE is = 

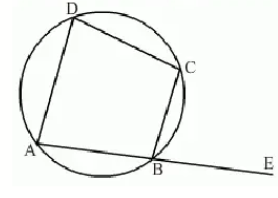
a)  100     b)  180      c)  160     d) 80

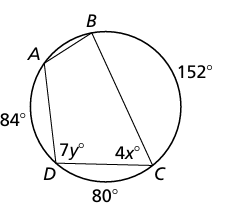
9. Find the values of x and y.

1. Answer :

By Theorem,

∠BAD + ∠BCD = 180°

Substitute ∠BCD = 100°.

∠BAD + 100° = 180°

Subtract 100° from each side. 

∠BAD = 80°

In triangle ABD,

∠ABD + ∠BAD + ∠ADB = 180°

50° + 80° + ∠ADB = 180°

130° + ∠ADB = 180°

Subtract 130° from each side.

∠ADB = 50°

2. Answer :

∠CAD :

The angles at the circumference subtended by the same arc are equal. ∠CAD and ∠CBD at the circumference subtended by the same arc CD.

∠CAD = ∠CBD

∠CAD = 30°

∠BCD :

By Theorem,

∠BAD + ∠BCD = 180°

In the above diagram, ∠BAD = ∠BAC + ∠CAD.

(∠BAC + ∠CAD) + ∠BCD = 180°

∠BAC + ∠CAD + ∠BCD = 180°

Substitute ∠BAC = 50° and ∠CAD = 30°.

50° + 30° + ∠BCD = 180°

80° + ∠BCD = 180°

Subtract 80° from each side. 

∠BCD = 100°

3. Answer :

By Theorem,

∠ABC + ∠ADC = 180°

Substitute ∠ADC = 120°.

∠ABC + 120° = 180°

Subtract 120° from each side. 

∠ABC = 60°

∠ACD = 90° (angle in a semi circle is a right angle)

In triangle ABC,

∠BAC + ∠ACB + ∠ABC = 180°

x° + 90° + 60° = 180°

x + 90 + 60 = 180

x + 150 = 180

Subtract 150 from each side.

x = 30

4. Answer :

∠BCD :

By Theorem,

∠BAC + ∠BCD = 180°

Substitute ∠BAD = 100°.

100° + ∠BCD = 180°

Subtract 100° from each side.

∠BCD = 80°

∠ADC :

Since AB || DC, AD is transversal.

When two parallel lines intersected by a transversal, same side interior angles are supplementary. 

∠BAD + ∠ADC = 180°

Substitute ∠BAD = 100°.

100° + ∠ADC = 180°

Subtract 100° from each side.

∠ADC = 80°

∠ABC :

By Theorem, 

∠ABC + ∠ADC = 180°

Substitute ∠ADC = 80°.

∠ABC + 80° = 180°

Subtract 80° from each side. 

∠ABC = 100°

5. Answer :

∠QPR : 

∠PRQ  =  90° (angle in a semi circle is a right angle)

In triangle PRQ,

∠PRQ + ∠QPR + ∠PQR = 180°

90° + ∠QPR + 55° = 180°

∠QPR + 145° = 180°

Subtract 145° from each side.

∠QPR = 35°

∠QPM : 

In triangle QPM,

∠QPM + ∠MQP + ∠QMP = 180°

∠QPM + 50° + 90° = 180°

∠QPM + 140° = 180°

Subtract 140° from each side. 

∠QPM = 40°

∠PRS : 

By Theorem,

∠PQR + ∠PSR = 180°

55° + ∠PSR = 180°

Subtract 55° from each side. 

∠PSR = 125°

In triangle PSR,

∠PSR + ∠SPR + ∠PRS = 180°

125° + 25° + ∠PRS = 180°

150° + ∠PRS = 180°

Subtract 150° from each side. 

∠PRS = 30°

6. Answer :

If ∠SQR = 80^o and ∠QPR = 30^o, find ∠SRQ.

Angles in the same segment they are equal.

<SPR = <SQR = 80

<QPR = <QSR = 30

In triangle SQR,

<QSR + <SRQ + <RQS = 180

30 + <SRQ + 80 = 180

110 + <SRQ = 180

<SRQ = 180 - 110

<SRQ = 70

7. Answer :

If ∠ACB = 50^o and ∠ABC = 110^o, find ∠BDC.

In triangle ABC,

<BAC + <ABC + <BCA = 180

<BAC + 110 + 50 = 180

<BAC + 160 = 180

<BAC = 180 - 160

<BAC = 20

<BAC = <BDC = 20 (angle in the same segment)

8. Answer :

Given <ADC = 80. The measure of <CBE is = 

Sum of opposite angles is equal to 180 degree

<ADC + <CBE = 180

80 + <CBE = 180

<CBE = 180 - 80

<CBE = 100

So, option a is correct.

9. Answer :

Angles subtended at the center of the arc is twice the angle at the circumference of the circle.

Arc of AB + Arc of BC + Arc of CD + Arc of DA = 360

Arc of AB + 152 + 80 + 84 = 360

Arc of AB + 316 = 360

Arc of AB = 360 - 316

Arc of AB = 44

2<ADC = Arc of AB + Arc BC

= 44 + 152 

2(7y) = 196

14y = 196

y = 196/14

y = 14

2<DCB = 84 + 44

2<DCB = 128

2(4x) = 128

8x = 128

x = 128/8

x = 16

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.