OPERATIONS WITH SCIENTIFIC NOTATION

Example 1 :

Simplify the expression given below. 

(4 x 10⁵) + (0.1 x 10⁷)

Solution : 

Method 1 :

Step 1 : 

In the given numbers, the highest power of 10 is 7. 

So, write each number with 10 power 7.

4 x 10⁵  =  0.04 x 10⁷

0.1 x 10⁷  =  0.1 x 10⁷

Step 2 : 

Add the multipliers for each number.

0.04 + 0.1  =  0.14

Step 3 : 

Write the final answer in scientific notation :

0.14 x 10⁷  =  1.4 x 10⁶

Method 2 :

Step 1 : 

First, write each number in standard notation.

4 x 10⁵  =  400,000

0.1 x 10⁷  =  1,000,000

Step 2 : 

Find the sum of the numbers in standard notation.

400,000 + 1,000,000  =  1,400,000

Step 3 : 

Write the final answer in scientific notation :

1,400,000  =  1.4 x 10⁶

Example 2 : 

Simplify the expression given below. 

(0.723 x 10⁸) + (338.2 x 10⁵) - (6.1 x 10⁷)

Solution :

Method 1 :

Step 1 : 

In the given numbers, the highest power of 10 is 8. 

So, write each number with 10 power 8.

0.723 x 10⁸  =  0.723 x 10⁸

338.2 x 10⁵  =  0.3382 x 10⁸

6.1 x 10⁷  =  0.61 x 10⁸

Step 2 : 

Simplify the multipliers.

0.723 + 0.3382 - 0.61  =  0.4512

Step 3 : 

Write the final answer in scientific notation :

0.4512 x 10⁸  =  4.512 x 10⁷

Method 2 :

Step 1 : 

First, write each number in standard notation.

0.723 x 10⁸  =  72,300,000

338.2 x 10⁵  =  33,820,000

6.1 x 10⁷  =  61,000,000

Step 2 : 

Simplify the numbers in standard notation.

72,300,000 + 33,820,000 - 61,000,000  =  45,120,000

Step 3 : 

Write the final answer in scientific notation :

45,120,000  =  4.512 x 10⁷

Example 3 :

Multiply :

(3.2 x 10⁵) x (26.7 x 10³)

Solution :

Step 1 :

Find the product of multipliers for each number. 

3.2 x 26.7  =  85.44

Step 2 :

Find the product of powers of 10.

10⁵ x 10³  =  10⁸

Step 3 :

Combine the results of step 1 and step 2 to write the final answer in scientific notation.

85.44 x 10⁸  =  8.544 x 10⁹

Example 4 :

When the Sun makes an orbit around the center of the Milky Way, it travels 2.025 × 10¹⁴ kilometers. The orbit takes 225 million years. At what rate does the Sun travel? Write your answer in scientific notation.

Solution :

Key points : 

The answer is the number of kilometers per year that the Sun travels around the Milky Way.

Set up a division problem using

Rate  =  Distance / Time

to represent the situation.

Step 1 : 

Substitute the values from the problem into the Rate formula. 

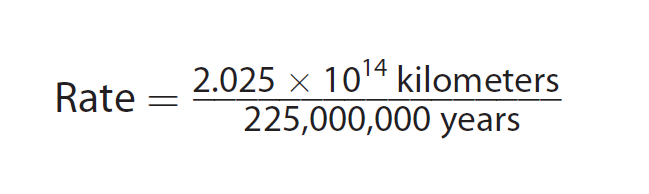
Step 2 : 

Write the expression for rate with years in scientific notation.

That is, 225 million  =  2.25 x 10⁸.

Then, we have

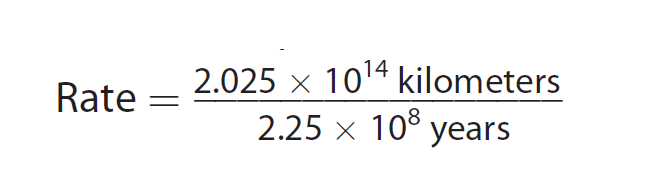
Step 3 :

Find the quotient by dividing the decimals and using the laws of exponents.

Divide the multipliers.

2.025 ÷  2.25  =  0.9

Divide the powers of 10.

10¹⁴ ÷ 10⁸  =  10^14-8

10¹⁴ ÷ 10⁸  =  10⁶

Step 4 :

Combine the answers to write the rate in scientific notation.

0.9 x 10⁶  =  9.0 x 10⁵

Justify and Evaluate : 

Use estimation to check the reasonableness of your answer.

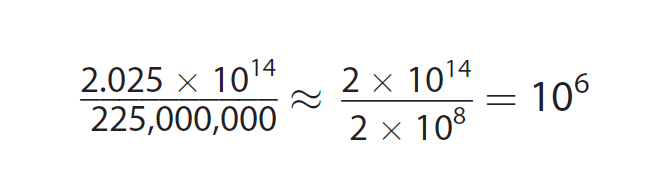
9.0 x 10⁵ is close 10⁶, so the answer is reasonable.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.