OPERATIONS WITH SCIENTIFIC NOTATION WORD PROBLEMS

Problem 1 : 

The table below shows the population of the three largest countries in North America in 2011. Find the total population of these countries.

Solution :

Method 1 :

Step 1 : 

First, write each population with the same power of 10.

United States : 3.1 x 10⁸

Canada : 0.338 x 10⁸

Mexico : 1.1 x 10⁸

Step 2 : 

Add the multipliers for each population.

3.1 + 0.338 + 1.1  =  4.538

Step 3 : 

Write the final answer in scientific notation :

4.538 x 10⁸

Method 2 :

Step 1 : 

First, write each number in standard notation.

United States : 310,000,000

Canada : 33,800,000

Mexico : 110,000,000

Step 2 : 

Find the sum of the numbers in standard notation.

310,000,000 + 33,800,000 + 110,000,000  =  453,800,000

Step 3 : 

Write the final answer in scientific notation :

453,800,000  =  4.538 x 10⁸

Problem 2 : 

Using the population table in the above example, how many more people live in Mexico than in Canada ? Write your answer in scientific notation.

Solution : 

7.62 x 10⁷ more people live in Mexico than in Canada.

Problem 3 :

When the Sun makes an orbit around the center of the Milky Way, it travels 2.025 × 10¹⁴ kilometers. The orbit takes 225 million years. At what rate does the Sun travel? Write your answer in scientific notation.

Solution : 

Key points : 

The answer is the number of kilometers per year that the Sun travels around the Milky Way.

Set up a division problem using

Rate  =  Distance / Time 

to represent the situation.

Step 1 : 

Substitute the values from the problem into the Rate formula. 

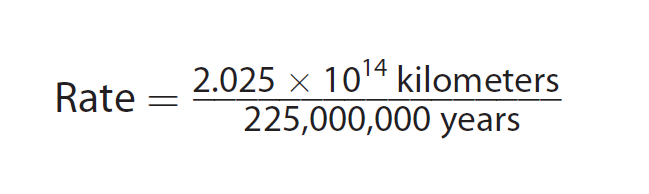
Step 2 : 

Write the expression for rate with years in scientific notation.

That is, 225 million  =  2.25 x 10⁸.

Then, we have

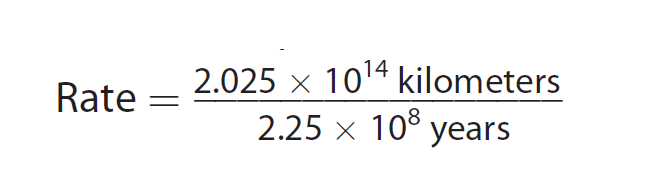
Step 3 :

Find the quotient by dividing the decimals and using the laws of exponents.

Divide the multipliers.

2.025 ÷  2.25  =  0.9 

Divide the powers of 10.

10¹⁴ ÷ 10⁸  =  10^14-8 

10¹⁴ ÷ 10⁸  =  10⁶ 

Step 4 :

Combine the answers to write the rate in scientific notation.

0.9 x 10⁶  =  9.0 x 10⁵

Justify and Evaluate : 

Use estimation to check the reasonableness of your answer.

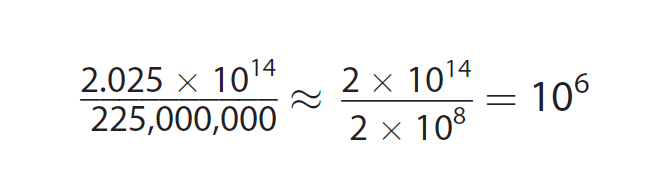
9.0 x 10⁵ is close 10⁶, so the answer is reasonable.

Reflect

1)  Light travels at a speed of 1.86 x 10⁵ miles per second. It takes light from the Sun about 4.8 × 10³ seconds to reach Saturn. Find the approximate distance from the Sun to Saturn. Write your answer in scientific notation.

2)  Light travels at the speed of 1.17 x 10⁷ miles per minute. Pluto’s average distance from the Sun is 3,670,000,000 miles. On average, how long does it take sunlight to reach Pluto? Write your answer in scientific notation.

Answers for the above questions : 

1)  8.928 × 10⁸ miles

2)  3.14 × 10² minutes

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.