OPERATIONS WITH POLYNOMIALS

A polynomial is an expression composed of coefficients and variables under addition, subtraction and multiplication and exponents on those variables must be non-negative integers. 

In Algebra, when we do stuff with polynomials, we must be aware of coefficient and like terms

Coefficient :

A numerical or constant quantity placed before and multiplied by the variable in an algebraic expression.

For example, in -4x the coefficient of x is -4.

Like Terms :

Like terms are terms that contain the same variables raised to the same power. Only the numerical coefficients are different. In an expression, only like terms can be combined.

For example, 5a, -3a, 2ab.

In the above three terms 5a and -3a are like terms, because they are having same variable, but 2ab is not like term of 5a or -3a, because it has a different variable 'ab' other than 'a'.

Writing Terms in Descending Order :

The terms of a polynomial in one variable are usually arranged by exponents in descending order, when read from left to right.

x³ + 7x² - 4x  + 2

The polynomial above contains one variable x. The terms of the polynomial are arranged by exponents in descending order. 

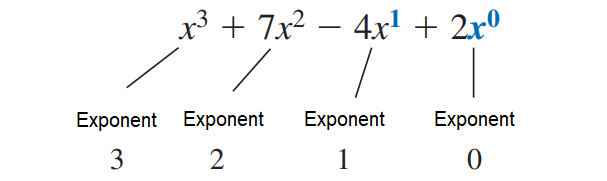
The following four operations with polynomials play a key role in Algebra.

1. Adding polynomials

2. Subtracting polynomials

3. Multiplying polynomials

4. Dividing polynomials

Adding Polynomials

Adding polynomials is combining the like terms. We can add polynomials either in vertical form or in horizontal form. 

Example 1 :

Add :

(5x² + 4x + 1) + (2x² + 5x + 2)

Solution :

In vertical form, arrange the like terms and add as shown below.  

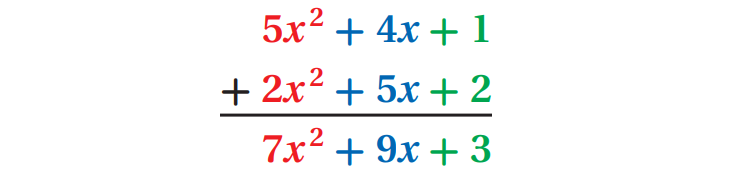
In horizontal form, we can use the Associative and Commutative Properties to regroup the like terms together and combine them as shown below.  

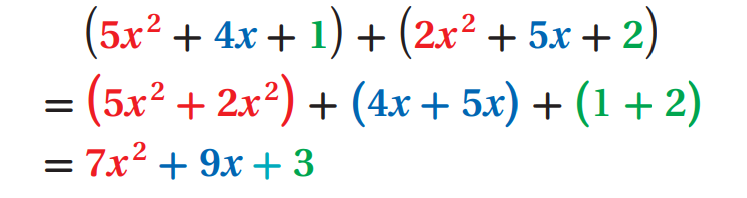
Subtracting Polynomials

Let A and B be two polynomials.

The following steps would be useful to subtract the polynomial B from A. 

Step 1 :

To subtract the polynomial B from polynomial A, write the polynomials in the form :

A - B

Step 2 : 

Use Distribute Property. 

That is, distribute negative sign to all the terms of polynomial B. 

Step 3 :

Group like terms together. 

Step 3 :

Combine like terms. 

Example 2 :

Subtract (2x² + 2y² - 6)  from  (3x² - 7y² + 9).

Solution : 

= (3x² - 7y² + 9) - (2x² + 2y² - 6)

Distributive Property. 

= 3x² - 7y² + 9 - 2x² - 2y² + 6

Group like terms together. 

= (3x² - 2x²) + (-7y² - 2y²) + (9 + 6)

Combine like terms. 

= x² - 9y² + 15

Multiplying Polynomials

Multiplying Monomials :

Product of powers property can be used to find the product of monomials. 

Product of Powers Property :

The product of two powers with the same base equals that base raised to the sum of the exponents. 

If x is any nonzero real number and m and n are integers, then

x^m ⋅ xⁿ  =  x^{m + n}

Example 3 :

Multiply. 

(3x³)(6x⁴)

Solution :

= (3x³)(6x⁴)

Group factors with like bases together. 

= (3 ⋅ 6)(x³ ⋅ x⁴)

Use the Product of Powers Property. 

= 18x^{3 + 4}

= 18x⁷

Multiplying Binomials :

You can use the following methods to multiply a binomial by a binomial.

(i) Distributive Property.

(ii) FOIL Method

Distributive Property :

To multiply a binomial by a binomial, Distributive Property can be used more than once.  

Example 4 : 

Multiply. 

(x + 3)(x - 6)

Solution : 

= (x + 3)(x - 6)

Distribute. 

= x(x - 6) + 3(x - 6)

Distribute again. 

= x(x) + x(-6) + 3(x) + 3(-6)

Multiply. 

= x² - 6x + 3x - 18

Combine like terms. 

= x² - 3x - 18

FOIL Method :

Another method for multiplying binomials is called the FOIL method. 

Example 5 : 

Multiply. 

(x + 4)(x + 5)

Solution : 

Multiply the First terms :

(x + 4)(x + 5) ---> x ⋅ x = x²

Multiply the Outer terms :

(x + 4)(x + 5) ---> x ⋅ 5 = 5x

Multiply the Inner terms :

(x + 4)(x + 5) ---> 4 ⋅ x = 4x

Multiply the Last terms :

(x + 4)(x + 5) ---> 4 ⋅ 5 = 20

(x + 4)(x + 5) = x² + 5x + 4x + 20

(x + 4)(x + 5) = x² + 9x + 20

Multiplying a Polynomial by a Monomial :

Using distributive property of multiplication, you can multiply a polynomial (a + b + c) by a monomial (a) as shown below.   

a(b + c + d) = a(b) + a(c) + a(d)

= ab + ac + ad

Example 6 : 

Multiply. 

5(3x² + 5x + 7)

Solution : 

= 5(3x² + 5x + 7)

Distribute 2.

= 5(3x²) + 5(5x) + 5(7)

Multiply. 

= 15x² + 25x + 35

Multiplying a Binomial by a Trinomial :

To multiply a binomial by a trinomial, you can use the Distributive Property several times. 

Example 7 :

Multiply.

(x + 3)(x² - 5x + 7)

Answer :

= (x + 3)(x² - 5x + 7)

Distributive. 

= x(x² - 5x + 7) + 3(x² - 5x + 7)

Distribute again. 

= x(x²) + x(-5x) + x(7) + 3(x²) + 3(-5x) + 3(7)

Simplify. 

= x³ - 5x² + 7x + 3x² - 15x + 21

Combine the like terms.

= x³ - 5x²  + 3x²+ 7x - 15x + 21

= x³ - 2x² - 8x + 21

Dividing Polynomials

Let p(x) and g(x) be two polynomials such that the degree of p(x) ≥ degree of g(x) and g(x) ≠ 0. Then there exists unique polynomials q(x) and r(x) such that

p(x) = g(x) ⋅ q(x) + r(x) ----(1)

where r(x) = 0 or degree of r(x) < degree of g(x). 

The polynomial p(x) is the Dividend, g(x) is the Divisor, q(x) is the Quotient and r(x) is the Remainder.

Now (1) can be written as

Dividend = (Divisor ⋅ Quotient) + Remainder

If r(x) is zero, then we say p(x) is a multiple of g(x). In other words, g(x) divides p(x).

If it looks complicated, don’t worry! it is important to know how to divide polynomials, and that comes easily with practice. The examples below will help you.

Example 8 : 

Divide (x³ - 4x² + 6x) by x, where x ≠ 0.

Solution : 

= (x³ - 4x² + 6x)/x

= x³/x - 4x²/x + 6x/x

= x² - 4x + 6

Example 9 : 

Divide (x² - 9) by (x - 3), where x ≠ 3.

Solution : 

= (x² - 9)/(x - 3)

= (x² - 3²)/(x - 3)

Using the algebraic identity a² - b² = (a + b)(a - b) to factor (x² - 3²). 

= [(x + 3)(x - 3)]/(x - 3)

= x + 3

Example 10 : 

Find the quotient and the remainder when (5x² - 7x + 2) is divided by (x - 1), using long division. 

Solution : 

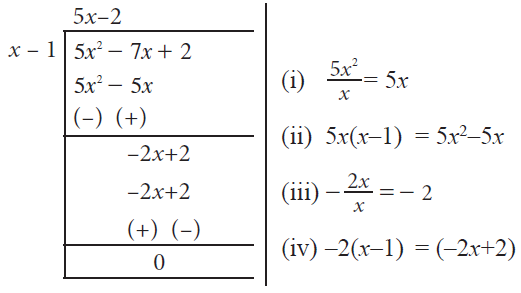
Quotient = 5x - 2

Remainder = 0

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.