OPERATIONS WITH NEGATIVE NUMBERS

Addition

In this section, we are going to see how to do addition when working with negative numbers. It can be done using a number line.

To add a positive number :

Move to the right on a number line

To add a negative number :

Move to the left on a number line

Example 1 :

Evaluate : -3 + 8.

Solution :

First number is -3 ----> start at -3.

A positive number 8 is added ----> move 8 units to the right of -3.

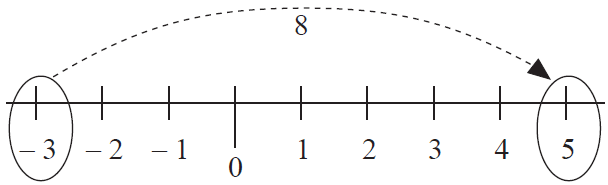
So, -3 + 8 = 5.

Example 2 :

Evaluate : 4 + (-2).

Solution :

First number is 4 ----> start at 4.

A negative number -2 is added ----> move 2 units to the left of 4.

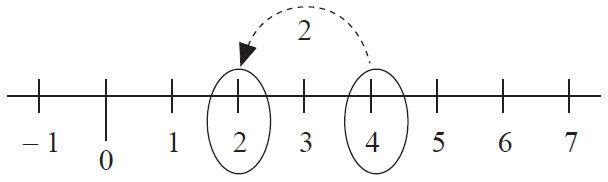
So, 4 + (-2) = 2.

Example 3 :

Evaluate : -8 + 5.

Solution :

First number is -8 ----> start at -8.

A positive number 5 is added ----> move 5 units to the right of -8.

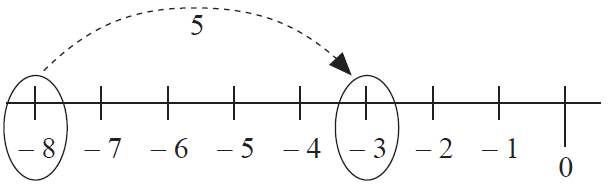
So, -8 + 5 = -3.

Example 4 :

Evaluate : -1 + (-3).

Solution :

First number is -1 ----> start at -1.

A negative number -3 is added ----> move 3 units to the left of -1.

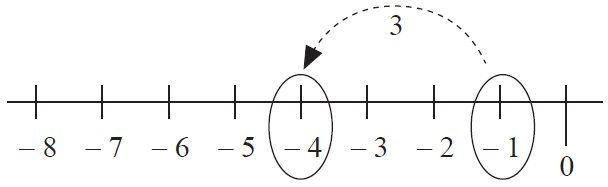
So, -1 + (-3) = -4.

Subtraction

In this section, we are going to see how to do subtraction when working with negative numbers. It can be done using a number line.

To subtract a positive number :

Move to the left on a number line

To subtract a negative number :

Move to the right on a number line

Example 5 :

Evaluate : 5 - 7.

Solution :

First number is 5 ----> start at 5.

A positive number 7 is subtracted ----> move 7 units to the left of 5.

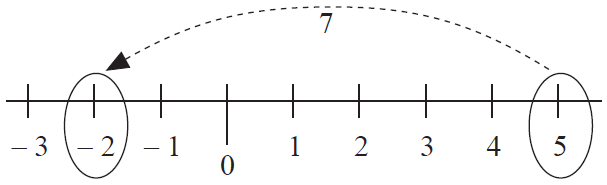
So, 5 - 7 = -2.

Example 6 :

Evaluate : 4 - (-2).

Solution :

First number is 4 ----> start at 4.

A negative number -2 is subtracted ----> move 2 units to the right of 4.

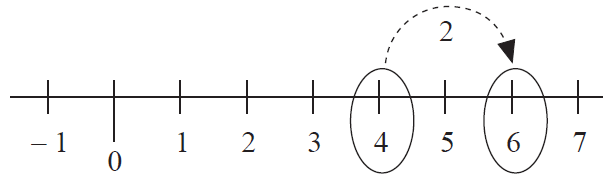
So, 4 - (-2) = 6.

Example 7 :

Evaluate : -2 - 3.

Solution :

First number is -2 ----> start at -2.

A positive number 3 is subtracted ----> move 3 units to the left of -2.

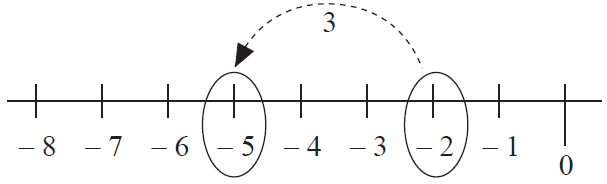
So, -2 - 3 = -5.

Example 8 :

Evaluate : -5 - (-3).

Solution :

First number is -5 ----> start at -5.

A negative number -3 is subtracted ----> move 3 units to the right of -5.

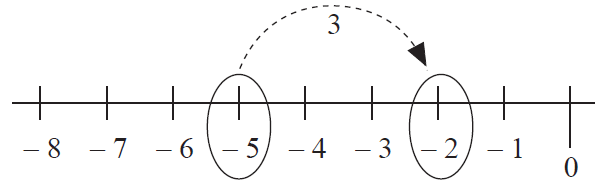
So, -5 - (-3) = -2.

Multiplication

In this section, we are going to see how to do multiplication when working with negative numbers. It can be done using a number line.

We can multiply the numbers as usual and decide the sign of the answer as shown below.

Positive x Negative = Negative

Negative x Positive = Negative

Negative x Negative = Positive

Example 9 :

Evaluate : 5 x (-7).

Solution :

5 times 7 is equal to 35.

Since a positive number is multiplied by a negative number, the answer is negative.

So, 5 x (-7) = -35.

Example 10 :

Evaluate : (-4) x 9.

Solution :

4 times 9 is equal to 36.

Since a negative number is multiplied by a positive number, the answer is negative.

So, (-4) x 9 = -36.

Example 11 :

Evaluate : (-3) x (-6).

Solution :

3 times 6 is equal to 18.

Since a negative number is multiplied by a negative number, the answer is positive.

So, (-3) x (-6) = 18.

Division

In this section, we are going to see how to do division when working with negative numbers. It can be done using a number line.

We can divide the numbers as usual and decide the sign of the answer as shown below.

Positive ÷ Negative = Negative

Negative ÷ Positive = Negative

Negative ÷ Negative = Positive

Example 12 :

Evaluate : 15 ÷ (-3).

Solution :

15 divided by 3 is equal to 5.

Since a positive number is divided by a negative number, the answer is negative.

So, 15 ÷ (-3) = -5.

Example 13 :

Evaluate : (-20) ÷ 5.

Solution :

20 divided by 5 is equal to 4.

Since a negative number is divided by a positive number, the answer is negative.

So, (-20) ÷ 5 = -4.

Example 14 :

Evaluate : (-28) ÷ (-4).

Solution :

28 divided by 4 is equal to 7.

Since a negative number is divided by a negative number, the answer is positive.

So, (-28) ÷ (-4) = 7.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

OPERATIONS WITH NEGATIVE NUMBERS

Addition

Subtraction

Multiplication

Division

Recent Articles

Digital SAT Math Problems and Solutions (part - 92)

SAT Math Resources (Videos, Concepts, Worksheets and More)

AP Calculus AB Problems with Solutions