OPERATIONS ON RATIONAL NUMBERS

Adding Rational Numbers

Adding Rational Numbers with Same Denominator :

To add two or more rational numbers with same denominator, we have to take the denominator once in common and add the numerators. 

Example :

Simplify : ⅕ + ⅖.

Adding Rational Numbers with Different Denominators :

To add two or more rational numbers with different denominators, we have to follow the steps given below. 

Step 1 :

Find the least common multiple of the denominators. 

Step 2 :

Make the denominators same using least common multiple and multiplication. 

Step 3 :

Take the denominator once in common and add the numerators. 

Example :

Simplify : ¼ + ⅙.

Least common multiple of (4, 6)  =  12

Multiply the numerator and denominator of the first rational number by 3 to get the denominator 12.

Multiply the numerator and denominator of the second rational number by 2 to get the denominator 12.

Subtracting Rational Numbers

Subtracting Rational Numbers with Same Denominator :

To subtract two rational numbers with same denominator, we have to take the denominator once in common and subtract the numerators. 

Example :

Simplify : ⅖ - ⅕.

Subtracting Rational Numbers with Different Denominators :

To subtract two rational numbers with different denominators, we have to follow the steps given below. 

Step 1 : 

Find the least common multiple of the denominators. 

Step 2 : 

Make the denominators same using least common multiple and multiplication. 

Step 3 : 

Take the denominator once in common and subtract the numerators. 

Example :

Simplify : ⅙ - ⅛.

Least common multiple of (6, 8)  =  24

Multiply the numerator and denominator of the first rational number by 4 to get the denominator 24.

Multiply the numerator and denominator of the second rational number by 3 to get the denominator 24.

Multiplying Rational Numbers

To multiply two or more rational numbers, we have to follow the steps given below. 

Step 1 : 

Simply any numerator with any denominator as much as possible.  

Step 2 : 

After simplification in step 1, multiply the numerator by numerator and denominator by denominator. 

Example :

Simplify : ⅚ x ¹⁸⁄₂₅.

Dividing Rational Numbers

To divide two rational numbers, we have to follow the steps given below. 

Step 1 : 

Change the division as multiplication and take the reciprocal for the second rational number.   

Step 2 : 

Simply any numerator with any denominator as much as possible.  

Step 2 : 

After simplification in step 2, multiply the numerator by numerator and denominator by denominator. 

Example :

Simplify : ⅔ ÷ ⁸⁄₁₅.

Distributive Property

(i) Distributive Property of Multiplication Over Addition :

Multiplication of rational numbers is distributive over addition.

Example :

Simplify : ⅓ x (⅖ + ⅕).

(ii) Distributive Property of Multiplication Over Subtraction :

Multiplication of rational numbers is distributive over subtraction.

Example :

Simplify : ⅓ x (⅖ - ⅕).

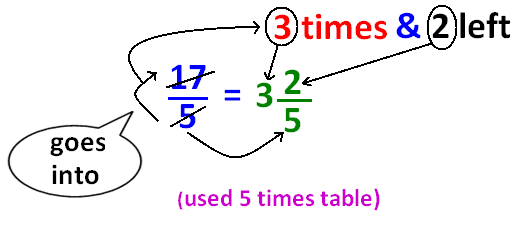
Converting Improper Fraction to Mixed Number

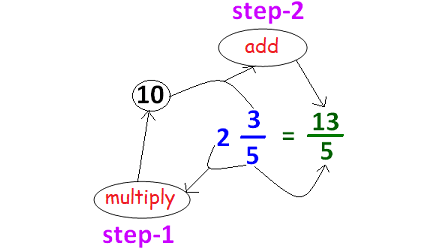
Converting Mixed Number to Improper Fraction

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.