OPERATION OF EVENTS IN PROBABILITY

Applying the concept of set theory, we can give a new dimension to the classical definition of probability.

A sample space may be defined as a non-empty set containing all the elementary events of a random experiment as sample points.

A sample space is denoted by S.

An event A may be defined as a non-empty subset of S. This is shown in the figure given below.

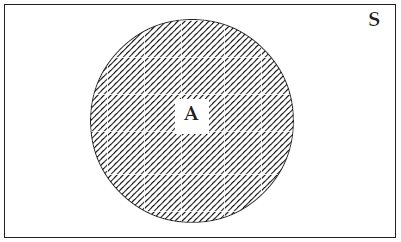
As for example, if a die is rolled once than the sample space is given by S = {1, 2, 3, 4, 5, 6}.

Next, if we define the events A, B and C such that

A = {x : x is an even no. of points in S}

B = {x : x is an odd no. of points in S}

C = {x : x is a multiple of 3 points in S}

Then, it is quite obvious that

A  =  {2, 4, 6}, B  =  {1, 3, 5} and C  =  {3, 6}

The classical definition of probability may be defined in the following way.

Let us consider a finite sample space S. That is, a sample space with a finite no. of sample points, n (S).

We assume that all these sample points are equally likely. If an event A which is a subset of S, contains n (A) sample points, then the probability of A is defined as the ratio of the number of sample points in A to the total number of sample points in S. 

P(A)  =  n(A)/n(S)

Union and Intersection of Two Events

Union of two events A and B is defined as a set of events containing all the sample points of event A or event B or both the events. This is shown in the figure given below.

And we have

AnB  =  { x : x ∈  A on x ∈ B } where x denotes the sample points.

Showing the union of two events A and B and also their intersection

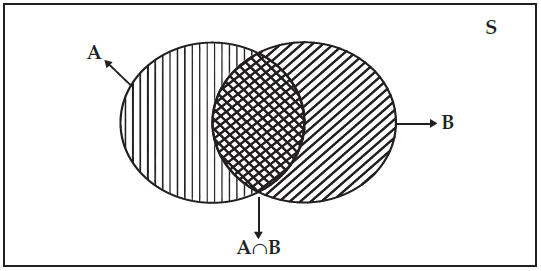
In the above example, we have

AUC  =  {2, 3, 4, 6} and AUB  =  {1, 2, 3, 4, 5, 6}

The intersection of two events A and B may be defined as the set containing all the sample points that are common to both the events A and B.

This is shown in the above figure. we have

AnB  =  { x : x∈A and x∈B }

In the above example, AnB  =  Null set

AnC  =  { 6 }

Since the intersection of the events A and B is a null set, it is obvious that A and B are mutually exclusive events as they cannot occur simultaneously.

Difference of Two Events

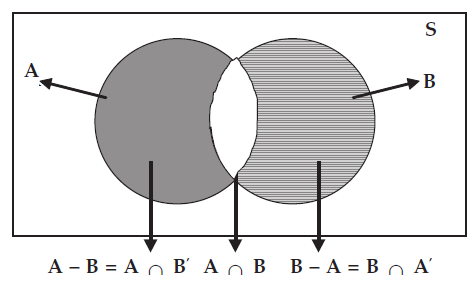
The difference of two events A and B, to be denoted by "A–B", may be defined as the set of sample points present in set A but not in B.

That is, 

A - B  =  { x : x∊A and x∉B }

Similarly, B - A  =  { x : x∊B and x∉A }

In the above examples, 

A - B  =  Null set and A - C  =  { 2, 4 }

This is shown in the figure given below.

Showing (A – B) and (B – A)

Complement of An Event

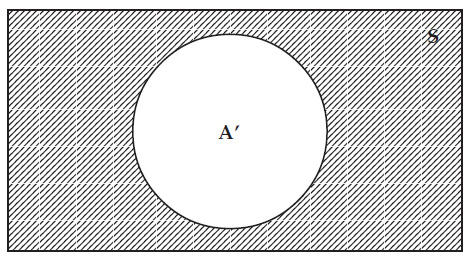
The complement of an event A may be defined as the difference between the sample space S and the event A.

A'  =  { x : x∊S and x∉A }

A'  =  S - A

A'  =  { 1, 3, 5 }

The figure given below depicts A'

Review

Now we are in a position to redefine some of the terms we have already discussed. 

Two events A and B are mutually exclusive if

P (AnB) = 0

Or more precisely, 

P(AuB)  =  P(A) + P(B)

Similarly three events A, B and C are mutually exclusive if

P(AuBuC)  =  P(A) + P(B) + P(C)

Two events A and B are exhaustive if

P(AuB)  =  1

Similarly three events A, B and C are exhaustive if

P(AuBuC)  =  1

Three events A, B and C are equally likely if

P(A)  =  P(B)  =  P(C)

Example

Question :

Three events A, B and C are mutually exclusive, exhaustive and equally likely.

What is the probably of the complementary event of A?

Solution :

Since A, B and C are mutually exclusive, we have

P(AuBuC)  =  P(A) + P(B) + P(C) ------ (1)

Since they are exhaustive,

P(AuBuC)  =  1 ------ (2)

Since they are equally likely events, 

P(A)  =  P(B)  =  P(C)  =  K, Say ------ (3)

Combining equations (1), (2) and (3), we have

1  =  K + K + K

1  =  3K

1/3  =   K

Thus P(A)  =  P(B)  =  P(C)  =  1/3

Therefore, P(A')  =  1 - P(A)

P(A')  =  1 - 1/3

P(A')  =  2/3

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.