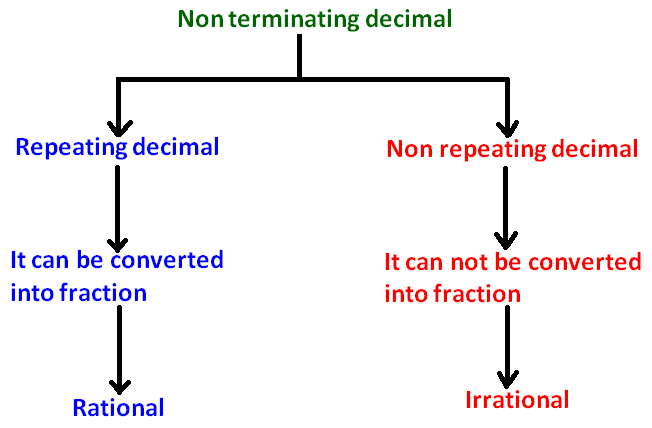
NON TERMINATING DECIMAL

What is  non terminating decimal ? 

A decimal number that continues infinitely or without end is called as non terminating decimal. 

Non terminating decimal - Types and properties

Repeating decimal - Examples 

23.562562562..........................(Repeated pattern is 562)

1.3333333333..........................(Repeated pattern is 3)

2.365636563656......................(Repeated pattern is 3656)

All the above decimal numbers are rational and they can be converted into fractions. 

How do we have this non terminating repeating decimal in math ? 

When we divide an integer by another integer, we may get the result in different forms. 

In those results, non terminating repeating decimal is one of the forms.

Let us consider the fraction 125 / 99.

When we divide 125 by 99, we get "Non terminating repeating decimal".  

It has been explained below. 

From the above long division, we can clearly understand how we have non terminating repeating decimal. 

Therefore,  125 / 99 = 1.262626..........................

When we divide 125 by 99, the digits after the decimal keep going infinitely and the repeated pattern is 26.  

Non repeating decimal - Examples 

All the above decimal numbers are irrational and they can not be converted into fractions. 

How do we have this non repeating decimal in math ?

When we are trying to find square of a number which is not a perfect square, we get this non repeating non terminating decimal. 

How to convert non terminating repeating decimal to fraction?

Step 1 : 

Let  x = Given decimal number 

For example,

If the given decimal number is 2.0343434.........

then, let x = 2.0343434...........

Step 2 : 

Identify the repeated pattern

For example,

In 2.0343434..........., the repeated pattern is 34

(Because 34 is being repeated)

Step 3 :

Identify the first repeated pattern and second repeated pattern as as explained in the example given below. 

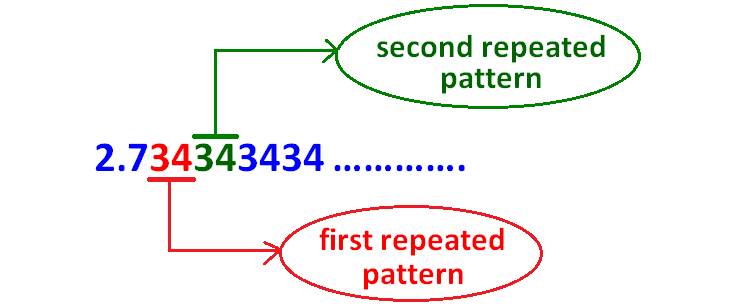
Step 4 :

Count the number of digits between the decimal point and first repeated pattern as given in the picture below. 

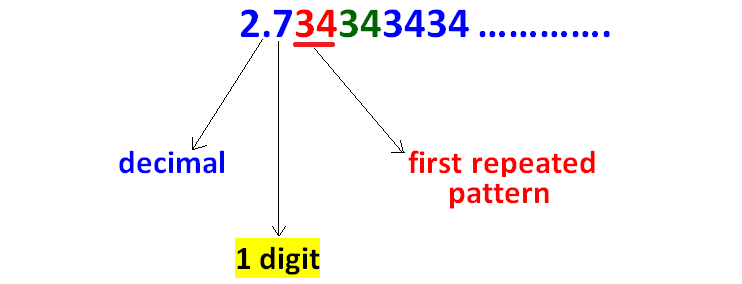
Step 5 :

Since there is 1 digit between the decimal point and the first repeated pattern, we have to multiply the given decimal by 10 as given in the picture below. 

(If there are two digits -----------> multiply by 100,

three digits -----------> multiply by 1000  and  so on )

Note : In (1), we have only repeated patterns after the decimal.

Step 6 : 

Count the number of digits between the decimal point and second repeated pattern as given in the picture below.

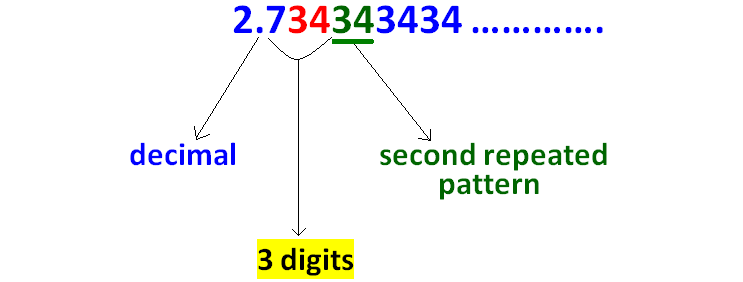
Step 7 :

Since there are 3 digits between the decimal point and the second repeated pattern, we have to multiply the given decimal by 1000 as given in the picture below. 

Note : In (2), we have only repeated patterns after the decimal.

Step 8 :

Now, we have to subtract the result of step 5 from step 7 as given in the picture below. 

Now we got the fraction which is equal to the given decimal

Some more problems

To have better understanding on conversion of non terminating repeating decimals to fraction, let us look at some problems.

Problem 1 :

Covert the given non terminating decimal into fraction

32.03256256256..........

Solution : 

Let X = 32.03256256256.............

Here, the repeated pattern is 256

No. of digits between the 1st repeated pattern and decimal = 2

So, multiply the given decimal by 100. Then, we have

100X = 3203.256256256...............----------(1) 

No. of digits between the 2nd repeated pattern and decimal = 5

So, multiply the given decimal by 100000. Then, we have

100000X = 3203256.256256256...............----------(2)

(2) - (1) --------> 99900X = 3200053

X = 3200053 / 99900

Hence, 32.03256256256.......... =  3200053 / 99900

Problem 2 :

Covert the given non terminating decimal into fraction

0.01232222........

Solution : 

Let X = 0.01232222.............

Here, the repeated pattern is 2

No. of digits between the 1st repeated pattern and decimal = 4

(Here, the first repeated pattern starts after four digits of the decimal)

So, multiply the given decimal by 10000. Then, we have

10000X = 123.2222...............----------(1) 

No. of digits between the 2nd repeated pattern and decimal = 5

So, multiply the given decimal by 100000. Then, we have

100000X = 1232.2222...............----------(2)

(2) - (1) --------> 90000X = 1109

X = 1109 / 90000

Hence, 0.01232222........... =  1109 / 90000

Problem 3 :

Covert the given non terminating decimal into fraction

2.03323232..........

Solution : 

Let X = 2.03323232.............

Here, the repeated pattern is 32

No. of digits between the 1st repeated pattern and decimal = 2

(Here, the first repeated pattern starts after two digits of the decimal)

So, multiply the given decimal by 100. Then, we have

100X = 203.323232...............----------(1) 

No. of digits between the 2nd repeated pattern and decimal = 4

So, multiply the given decimal by 10000. Then, we have

10000X = 20332.323232...............----------(2)

(2) - (1) --------> 9900X = 20129

X = 9900 / 20129

Hence, 2.03323232.......... =  9900 / 20129

Problem 4 :

Covert the given non terminating decimal into fraction

0.252525..........

Solution : 

Let X = 0.252525.............

Here, the repeated pattern is 25

No. of digits between the 1st repeated pattern and decimal = 0 

So, multiply the given decimal by 1. Then, we have

X = 0.252525...............----------(1) 

No. of digits between the 2nd repeated pattern and decimal = 2

So, multiply the given decimal by 100. Then, we have

100X = 25.252525...............----------(2)

(2) - (1) --------> 99X = 25

X = 25 / 99

Hence, 0.252525.......... =  25 / 99

Problem 5 :

Covert the given non terminating decimal into fraction

3.3333..........

Solution : 

Let X = 3.3333.............

Here, the repeated pattern is 3

No. of digits between the 1st repeated pattern and decimal = 0

(Here, the first repeated pattern is "3" which comes right after the decimal point)

So, multiply the given decimal by 1. Then, we have

X = 3.3333...............----------(1) 

No. of digits between the 2nd repeated pattern and decimal = 1

(Here, the second repeated pattern is "3" which comes one digit  after the decimal point)

So, multiply the given decimal by 10. Then, we have

10X = 33.3333...............----------(2)

(2) - (1) --------> 9X = 30

X = 30 / 9 = 10 / 3

Hence, 3.3333.............. =  10 / 9

Problem 6 :

Covert the given non terminating decimal into fraction

1.023562562562..........

Solution : 

Let X = 1.023562562562.............

Here, the repeated pattern is 562

No. of digits between the 1st repeated pattern and decimal = 3 

So, multiply the given decimal by 1000. Then, we have

1000X = 1023.562562562...............----------(1) 

No. of digits between the 2nd repeated pattern and decimal = 6

So, multiply the given decimal by 1000000. Then, we have

1000000X = 1023562.562562562...............----------(2)

(2) - (1) --------> 999000X = 1022538

X = 1022539 / 999000 

Hence, 1.023562562562.......... =  1022539 / 999000