NETS AND SURFACE AREA
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
A net is a two-dimensional pattern of shapes that can be folded into a three-dimensional figure. The shapes in the net become the sides, or faces, of the three-dimensional figure.
Example 1 :
Find the surface area of the square pyramid given below.
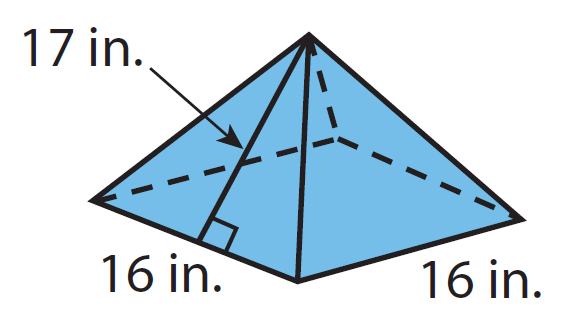
Solution :
Make a net of this square pyramid, and use the net to find the surface area.
Step 1 :
Make a net of the pyramid.
Draw the square base, draw a triangle on each side and label the dimensions.
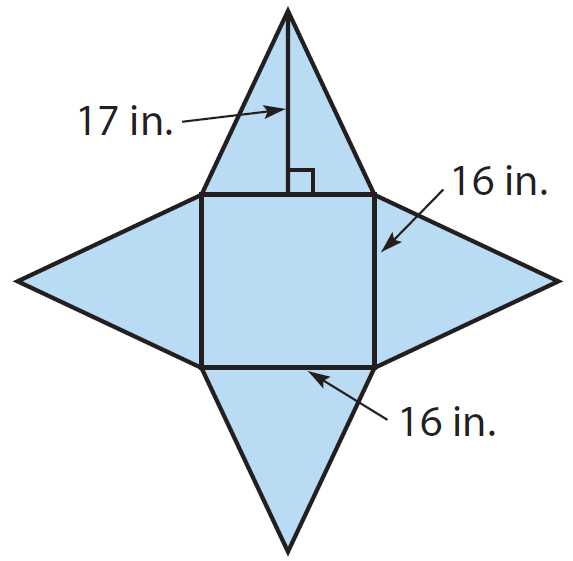
Step 2 :
Use the net to find the surface area.
There are four triangles with base 16 in. and height 17 in.
The area of the 4 triangles is
= 4 x (1/2) x 16 x 17
= 544 in2
The area of the base is
= 16 x 16
= 256 in2
Hence, the required surface area is
= 544 + 256
= 800 in2
Example 2 :
A sculpture sits on pedestal in the shape of a square prism. The side lengths of a base of the prism are 3 feet. The height of the prism is 4 feet. The museum director wants to cover all but the underside of the pedestal with foil that costs $0.22 per square foot. How much will the foil cost?
Solution :
From the given information, we have the following figure.
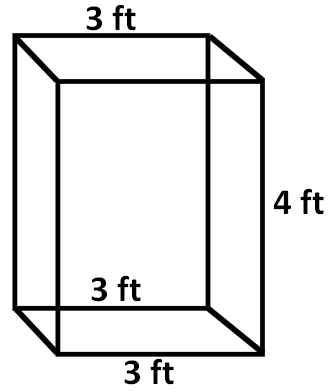
Step 1 :
Use a net to show the faces that will be covered with foil.
Draw the top.
Draw the faces of the prism that are connected to the top.
We don’t need to include the bottom of the pedestal.
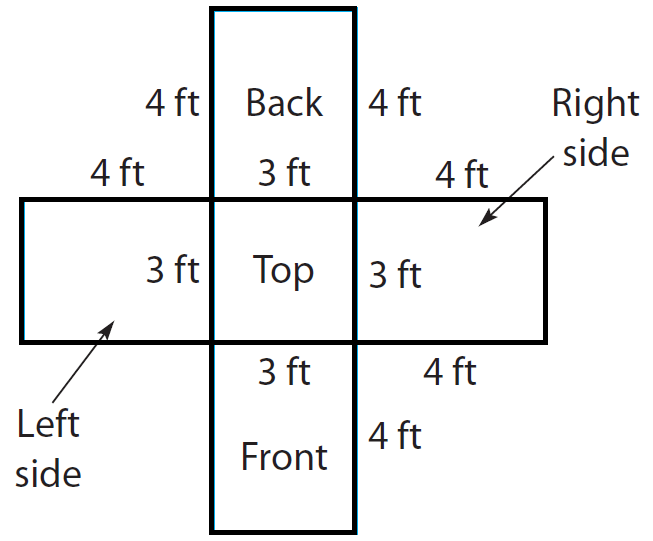
Step 2 :
Use a net to show the faces that will be covered with foil.
Use the net to find the area that will be covered with foil.
Area of top = 3 x 3
= 9 ft2
The other four faces are identical.
Area of four faces = 4 x 3 x 4
= 48 ft2
Area to be covered = 9 + 48
= 57 ft2
Step 2 :
Find the cost of the foil.
57 x $0.22 = $12.54
The foil will cost $12.54.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 45)
Jan 19, 26 06:14 AM
10 Hard SAT Math Questions (Part - 45) -
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations
