COMPARING COEFFICIENTS OF LINEAR EQUATIONS IN TWO VARIABLES AND SOLVING
To compare the coefficients of linear equations in two variables, the equations must be in the form.
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
The following three cases are possible for any given system of linear equations.
(i) a1/a2 ≠ b1/b2, we get a unique solution
(ii) a1/a2 = a1/a2 = c1/c2, there are infinitely many solutions.
(iii) a1/a2 = a1/a2 ≠ c1/c2, there is no solution
Problems :
Which of the following pairs of linear equations are consistent/inconsistent? if consistent, obtain the solution graphically.
(i) x + y = 5
2 x + 2 y = 10
Solution :
x + y - 5 = 0
2 x + 2 y - 10 = 0
From the given equations, let us find the values of a1, a2, b1, b2, c1 and c2
a1 = 1, b1 = 1, c1 = -5
a2 = 2, b2 = 2, c2 = -10
a1/a2 = 1/2 -------(1)
b1/b2 = 1/2 -------(2)
c1/c2 = -5/(-10) = 1/2 -------(3)
This exactly matches the condition,
a1/a2 = b1/b2 = c1/c2
So, the system of equations will have infinitely many solution.
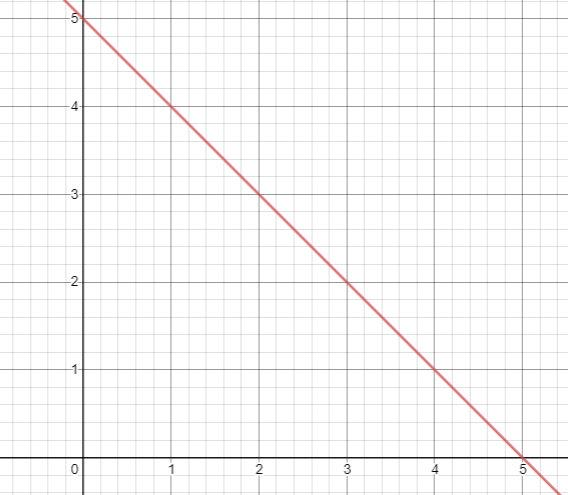
To draw the graph, let us find x and y intercepts.
x + y - 5 = 0
|
To find x - intercept : Put y = 0 x - 5 = 0 x = 5 (5, 0) |
To find y - intercept : Put x = 0 y - 5 = 0 y = 5 (0, 5) |
Both equations are representing the same line.
(ii) x - y = 8
3 x - 3 y = 16
Solution :
x - y – 8 = 0
3 x - 3 y -16 = 0
From the given equations, let us find the values of a1, a2, b1, b2, c1 and c2
a1 = 1, b1 = -1, c1 = -8
a2 = 3, b2 = -3, c2 = -16
a1/a2 = 1/3 -------(1)
b1/b2 = (-1)/(-3) = 1/3 -------(2)
c1/c2 = -8/(-16) = 1/2 -------(3)
This exactly matches the condition
a1/a2 = b1/b2 ≠ c1/c2
So, there is no solution.
(iii) 2 x + y - 6 = 0
4 x - 2 y - 4 = 0
Solution :
From the given equations, let us find the values of a1, a2, b1, b2, c1 and c2
a1 = 2, b1 = 1, c1 = -6
a2 = 4, b2 = -2, c2 = -4
a1/a2 = 2/4 = 1/2 -------(1)
b1/b2 = 1/(-2) = -1/2 -------(2)
c1/c2 = -6/(-4) = 3/2 -------(3)
This exactly matches the condition a1/a2 ≠ b1/b2
So, it has unique solution.
Graphing 1st equation,
2 x + y - 6 = 0
y = -2x + 6
|
x-intercept : Put y = 0 -2x + 6 = 0 -2x = -6 x = 3 (3, 0) |
y-intercept : Put x = 0 y = -2(0) + 6 y = 6 (0, 6) |
Graphing 2nd equation,
4 x - 2 y - 4 = 0
2y = 4x - 4
y = 2x - 2
|
x-intercept : Put y = 0 2x - 2 = 0 2x = 2 x = 1 (1, 0) |
y-intercept : Put x = 0 y = 2(0) - 2 y = -2 (0, -2) |
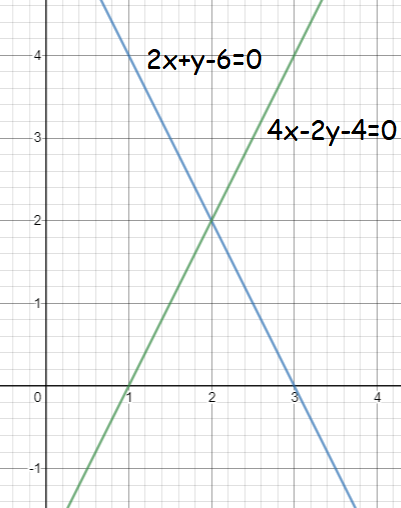
The above lines are intersecting at the point (2, 2). So, the solution is x = 2 and y = 2.
(iv) 2 x - 2 y - 2 = 0
4 x - 4 y - 5 = 0
Solution :
From the given equations, let us find the values of a1, a2, b1, b2, c1 and c2
a1 = 2, b1 = -2, c1 = -2
a2 = 4, b2 = -4, c2 = -5
a1/a2 = 2/4 = 1/2 -------(1)
b1/b2 = -2/(-4) = 1/2 -------(2)
c1/c2 = -2/(-5) = 2/5 -------(3)
This exactly matches the condition a1/a2 = b1/b2 ≠ c1/c2
This exactly matches the condition
a1/a2 = b1/b2 ≠ c1/c2
So, there is no solution.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Factoring Trinomials Worksheet
Apr 25, 24 08:40 PM
Factoring Trinomials Worksheet -
Factoring Quadratic Trinomials Worksheet
Apr 25, 24 08:13 PM
Factoring Quadratic Trinomials Worksheet -
Factoring Quadratic Trinomials
Apr 25, 24 07:03 PM
Factoring Quadratic Trinomials - Methods - Solved Examples

